在估计问题中一般有无穷多个行动可供选择,对这类问题使用贝叶斯统计决策方法是很容易解决的。例如,行动空间由 $r$ 个行动组成,即 $\mathscr{A}={a_1,\dots,a_r}$。设在采取行动 $a_i$ 下的损失为 $L(\theta,a_i),i=1,\dots,r$,则贝叶斯决策就是选择使后验风险 $R(a_i\mid\pmb x)$ 达到最小的那个行动。
假设检验问题
设 $X\sim f(x\mid\theta)$,$\theta$的先验分布为 $\pi(\theta)$,$\pmb X=(X_1,\dots,X_n)$ 为从总体 $X$ 中抽取的i.i.d.样本,则 $\theta$ 的后验分布为
$\pi(\theta\mid\pmb x)=\dfrac{f(\pmb x\mid\theta)\pi(\theta)}{\int_{\Theta}f(\pmb x\mid\theta)\pi(\theta){\rm d}\theta}.$
待考察的假设检验问题为
$H_0:\theta\in\Theta_0\longleftrightarrow H_1:\theta\in\Theta_1,\quad\Theta_0\cup\Theta_1=\Theta.$
决策行动:$a_0$ 表示接受 $H_0$;$a_1$ 表示否定 $H_0$,接受 $H_1$。
定理. 设总体 $X\sim f(x\mid\theta),\theta\in\Theta=\Theta_0\cup\Theta_1$,$\theta$ 的先验分布为
$\pi(\theta)=\left\{\begin{array}{ll}
\pi_0g_0(\theta), & \theta\in\Theta_0,\\
\pi_1g_1(\theta), & \theta\in\Theta_1.
\end{array}\right.$
设 $\pmb X=(X_1,\dots,X_n)$ 为从总体 $X$ 中抽取的i.i.d.样本,损失函数
$L(\theta,a_i)=\left\{\begin{array}{ll}
0, & \theta\in\Theta_i,\\
k_i(\theta), & \theta\notin\Theta_i,
\end{array}\right.$
其中 $i=0,1$,且 $k_0(\theta),k_1(\theta)$ 为正函数。则贝叶斯决策函数为
$\delta(\pmb x)=\left\{\begin{array}{ll}
0, & \pmb x\notin W,\\ 1, & \pmb x\in W,
\end{array}\right.$
其中拒绝域 $W$ 为
$\displaystyle W=\left\{\pmb x:\pi_0\int_{\Theta_0}k_1(\theta)f(\pmb x\mid\theta)g_0(\theta){\rm d}\theta<\pi_1\int_{\Theta_1}k_0(\theta)f(\pmb x\mid\theta)g_1(\theta){\rm d}\theta\right\}.$
设 $\pi(\theta\mid\pmb x)$ 为 $\theta$ 的后验分布,则决策函数 $a_i(i=0,1)$ 的后验风险为
$\displaystyle R(a_i\mid\pmb x)=\mathcal{E}_{\theta\vert\pmb x}[L(\theta,a)]=\int_{\Theta_{1-a}}k_{a}(\theta)\pi(\theta\mid\pmb x){\rm d}\theta=\dfrac{\pi_{1-a}}{m(\pmb x)}\int_{\Theta_{1-a}}k_{a}(\theta)f(\pmb x\mid\theta)g_{1-a}(\theta){\rm d}\theta$
按后验风险最小原则,上述定理便得到证明。下面考虑几种特殊的情形:
0-1损失
若损失函数为0-1损失
$L(\theta,a_i)=\left\{\begin{array}{ll}
0, & \theta\in\Theta_i,\\
1, & \theta\notin\Theta_i,
\end{array}\right.\quad i=0,1,$
则后验风险为
$\displaystyle R(a_0\mid\pmb x)=\mathbb P(\theta\in\Theta_1\mid\pmb x),\quad R(a_1\mid\pmb x)=\mathbb P(\theta\in\Theta_0\mid\pmb x).$
因此按后验风险最小原则,对应的贝叶斯决策就是接受具有较大后验概率的假设,这与贝叶斯统计推断中的结论是一致的。

0-$k_i$ 损失
若损失函数为0-$k_i$ 损失
$L(\theta,a_i)=\left\{\begin{array}{ll}
0, & \theta\in\Theta_i,\\
k_i, & \theta\notin\Theta_i,
\end{array}\right.\quad i=0,1,$
则后验风险为
$\displaystyle R(a_0\mid\pmb x)=k_0\mathbb P(\theta\in\Theta_1\mid\pmb x),\quad R(a_1\mid\pmb x)=k_1\mathbb P(\theta\in\Theta_0\mid\pmb x).$
因此按后验风险最小原则,若 $\mathbb P(\theta\in\Theta_1\mid\pmb x)\geq\dfrac{k_1}{k_0+k_1}$,则否定 $H_0$,否则接受 $H_0$。

多决策问题
对于多决策问题,待考察的假设检验问题为
$H_i:\theta\in\Theta_i,\quad i=1,2,\dots,r.$
考虑损失函数为
$L(\theta,a_i)=\left\{\begin{array}{ll}
0, & \theta\in\Theta_i,\\
k_{ij}(\theta), & \theta\in\Theta_j(j\neq i),
\end{array}\right.\quad i=1,\dots,r,$
则后验风险为
$\displaystyle R(a_i\mid\pmb x)=\int_{\Theta}L(\theta,a_i)\pi(\theta\mid\pmb x){\rm d}\theta=\sum_{j=1}^r\int_{\Theta_j}k_{ij}(\theta)\pi(\theta\mid\pmb x){\rm d}\theta.$
因此按后验风险最小原则,取后验风险最小的那个决策为贝叶斯决策。
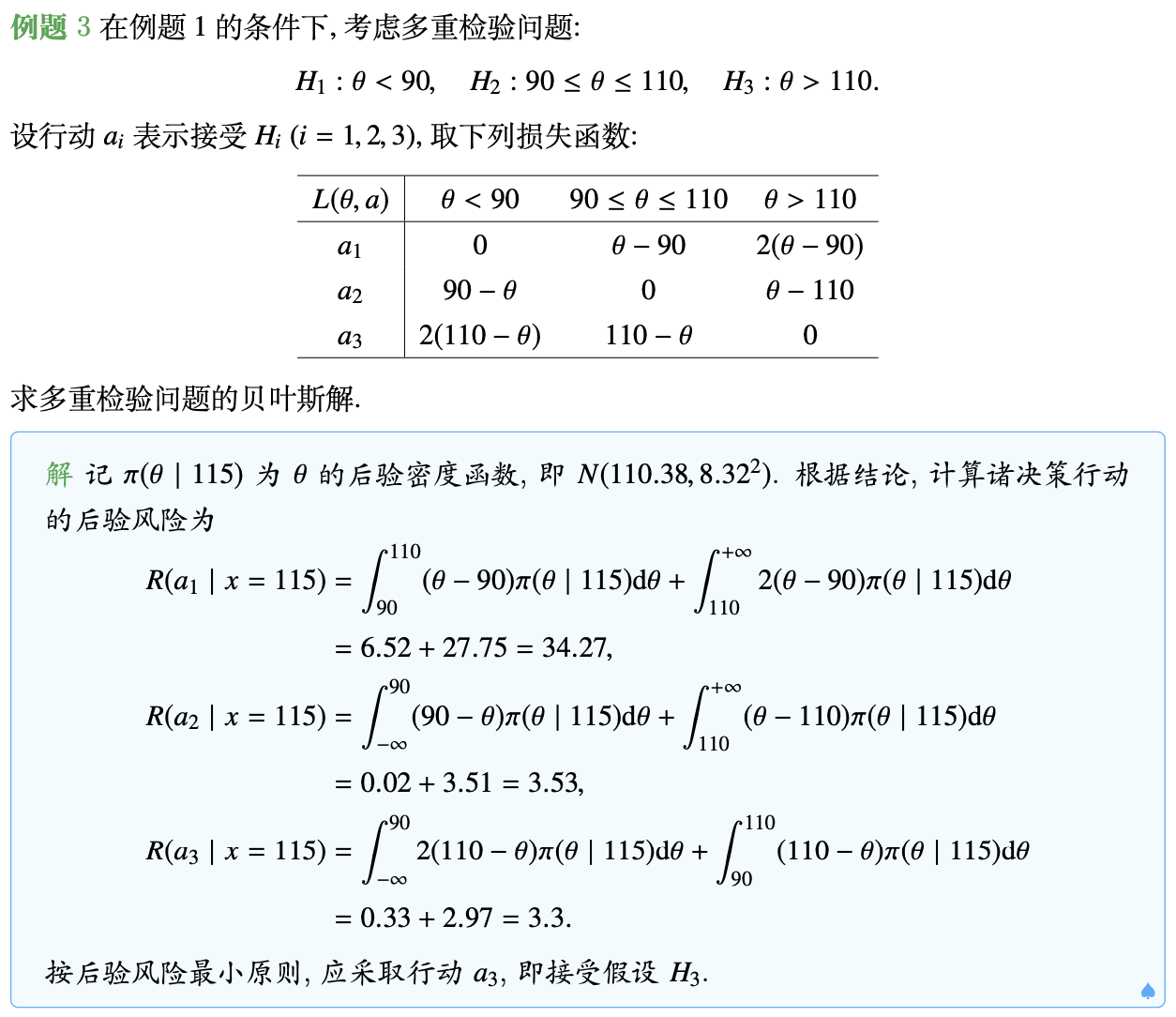
区间估计问题
设 $C(\pmb x)=(d_1(\pmb x),d_2(\pmb x))$ 为 $\theta$ 的一个区间估计,损失函数的一种取法为
$L(\theta,C(\pmb x))=m_1\big[d_2(\pmb x)-d_1(\pmb x)\big]+m_2\big[1-I\{\theta\in C(\pmb x)\}\big].$
按后验风险的原则,应使区间估计的后验风险
$R(C(\pmb x)\mid\pmb x)=m_1\big[d_2(\pmb x)-d_1(\pmb x)\big]+m_2\mathbb P_{\theta\vert\pmb x}(\theta\notin C(\pmb x))$
越小越好,但是要找出最优解并非易事,优化问题能够得以解决的不多。
Minimax准则
对一个统计决策问题,为选定一个较优的决策函数,需要建立反映决策函数优劣的指标。风险函数 $R(\theta,\delta)=\mathbb E[L(\theta,\delta(\pmb X)]$ 就是这样的指标,即采取决策函数 $\delta(\pmb x)$ 而参数真值为 $\theta$ 时所蒙受的平均损失。风险函数越小,决策函数越好。
前面已经介绍,对决策函数 $\delta(\pmb x)$,若不存在一致优于它的决策函数,则称 $\delta(\pmb x)$ 为可容许的决策函数。不过一般情况下,可容许的决策函数不存在,我们往往需要放宽对决策函数的要求,由此引出了不同的决策准则——之前我们关注的重点在贝叶斯准则。下面我们来看Minimax准则。
Minimax决策准则是基于最大风险 $R_M(\delta(\pmb x))=\max\limits_{\theta\in\Theta}R(\theta,\delta(\pmb x))$ 的准则。
定义. 若存在决策函数 $\delta^\star(\pmb x)$,使得
$R_M(\delta^\star(\pmb x))=\min\limits_{\delta(\pmb x)\in\mathscr{A}}R_M(\delta(\pmb x)),$
即对一切决策函数 $\delta(\pmb x)$ 都有 $R_M(\delta^\star(\pmb x))\leq R_M(\delta(\pmb x))$,则称 $\delta^\star(\pmb x)$ 是在参数空间 $\Theta$ 上 $\theta$ 的Minimax估计或Minimax解。
然而,求Minimax解通常比较困难。下面三个定理给出了验证某一特定的解为Minimax解的方法。
定理. 设 $\hat{\delta}(\pmb x)$ 为在先验分布 $\pi(\theta)$ 之下 $\theta$ 的贝叶斯估计,并且 $\hat{\delta}(\pmb x)$ 的风险函数 $R(\theta,\hat{\delta}(\pmb x))$ 以它的贝叶斯风险 $R_\pi(\hat{\delta}(\pmb x))$ 为上界,即
$R(\theta,\hat{\delta}(\pmb x))\leq R_\pi(\hat{\delta}(\pmb x))=\min\limits_{\delta(\pmb x)\in\mathscr{A}}R_\pi(\delta(\pmb x)),\quad\forall\theta\in\Theta,$
则 $\hat{\delta}(\pmb x)$ 为 $\theta$ 的Minimax估计。
证明: 假设 $\hat{\delta}(\pmb x)$ 不是 $\theta$ 的Minimax估计,则存在 $\theta$ 的另一个估计 $\hat{\delta}_0(\pmb x)\neq\hat{\delta}(\pmb x)$,使得
$\max\limits_{\theta\in\Theta}R(\theta,\hat{\delta}_0(\pmb x))<\max\limits_{\theta\in\Theta}R(\theta,\hat{\delta}(\pmb x))$
此时有
$\begin{array}{rl}
R_\pi(\hat{\delta}_0(\pmb x)) =&\!\!\!\! \displaystyle\int_{\Theta}R(\theta,\hat{\delta}_0(\pmb x))\pi(\theta){\rm d}\theta\leq\max\limits_{\theta\in\Theta}R(\theta,\hat{\delta}_0(\pmb x))\\
<&\!\!\!\!\max\limits_{\theta\in\Theta}R(\theta,\hat{\delta}(\pmb x))\leq R_\pi(\hat{\delta}(\pmb x))=\min\limits_{\delta(\pmb x)\in\mathscr{A}}R_\pi(\delta(\pmb x)),
\end{array}$
则 $\hat{\delta_0}(\pmb x)$ 的贝叶斯风险比 $\hat{\delta}(\pmb x)$ 的贝叶斯风险小,这与条件 $R_\pi(\hat{\delta}(\pmb x))=\min\limits_{\delta(\pmb x)\in\mathscr{A}}R_\pi(\delta(\pmb x))$ 矛盾。
特别地,如果 $\hat{\delta}(\pmb x)$ 的风险函数为常数,则有如下定理。
定理. 设 $\hat{\delta}(\pmb x)$ 为在先验分布 $\pi(\theta)$ 之下 $\theta$ 的贝叶斯估计,若 $\hat{\delta}(\pmb x)$ 的风险函数为常数 $c$,即
$R(\theta,\hat{\delta}(\pmb x))\equiv c,\quad\forall\theta\in\Theta,$
则 $\hat{\delta}(\pmb x)$ 为 $\theta$ 的Minimax估计。

然而,一般很难找到一个其风险函数为常数的贝叶斯解。下面定理的应用要广泛得多。
定理. 设 $\hat{\delta_k}(\pmb x)$ 为在先验分布 $\pi_k(\theta)$ 之下 $\theta$ 的一列贝叶斯估计,$k=1,2,\dots$;假定 $\hat{\delta_k}(\pmb x)$ 的贝叶斯风险为 $R_{\pi_k}(\hat{\delta_k}(\pmb x))$,$k=1,2,\dots$,且有
$\lim\limits_{k\rightarrow\infty}R_{\pi_k}(\hat{\delta}_k(\pmb x))=r<\infty,$
又设 $\hat{\delta}^\star(\pmb x)$ 为 $\theta$ 的一个估计量,它的最大风险 $R_M(\hat{\delta}^\star(\pmb x))$ 满足条件
$R_M(\hat{\delta}^\star(\pmb x))\leq\lim\limits_{k\rightarrow\infty}R_{\pi_k}(\hat{\delta}_k(\pmb x))=r,$
则 $\hat{\delta}^\star(\pmb x)$ 为 $\theta$ 的Minimax估计。
证明: 假设 $\hat{\delta}^\star(\pmb x)$ 不是 $\theta$ 的Minimax估计,则存在 $\theta$ 的另一个估计 $\hat{\delta}_0(\pmb x)\neq\hat{\delta}^\star(\pmb x)$,使得
$\max\limits_{\theta\in\Theta}R(\theta,\hat{\delta}_0(\pmb x))<\max\limits_{\theta\in\Theta}R(\theta,\hat{\delta}^\star(\pmb x))\leq r=\lim\limits_{k\rightarrow\infty}R_{\pi_k}(\hat{\delta}_k(\pmb x)),$
则存在充分大的 $k_0$,使得
$\max\limits_{\theta\in\Theta}R(\theta,\hat{\delta}_0(\pmb x))<R_{\pi_{k_0}}(\hat{\delta}_{k_0}(\pmb x)).$
此时有
$R_{\pi_{k_0}}(\hat{\delta}_0(\pmb x))=\displaystyle\int_{\Theta}R(\theta,\hat{\delta}_0(\pmb x))\pi_{k_0}(\theta){\rm d}\theta\leq\max_{\theta\in\Theta}R(\theta,\hat{\delta}_0(\pmb x))<R_{\pi_{k_0}}(\hat{\delta}_{k_0}(\pmb x)),$
则在先验分布 $\pi_k(\theta)$ 下,$\hat{\delta_0}(\pmb x)$ 的贝叶斯风险比 $\hat{\delta_{k_0}}(\pmb x)$ 的贝叶斯风险小,这与条件 $\hat{\delta_{k_0}}(\pmb x)$ 是先验分布 $\pi_k(\theta)$ 下的贝叶斯解矛盾。

后记
本文内容参考自中国科学技术大学《贝叶斯分析》(2022Fall)课件。
如对本文内容有任何疑问,请联系 watthu@mail.ustc.edu.cn。




