介绍
在实际应用背景下,强化学习的行动空间 $\mathcal A$ 和状态空间 $\mathcal S$ 都可能十分巨大,如果要保存值函数的所有可能值(或者说要对每个状态都进行学习),除了存储空间比较大,计算时间也比较长,因此需要寻找近似的函数——具体可以使用线性组合、神经网络以及其他方法来近似值函数。
-
利用监督学习里的数据拟合方法去估计值函数
$\hat{v}(s,\pmb w)\approx v_\pi(s),\quad\hat{q}(s,a,\pmb w)\approx q_\pi(s,a).$ - 数据拟合方法具有泛化能力,一些没出现过的状态也有可能被正确估计。
- 可以利用蒙特卡洛学习或时序差分学习方法来更新参数 $\pmb w$。
通过这种函数近似,可以用少量的参数 $\pmb w$ 来拟合实际的各种价值函数。
强化学习应用的场景中,其数据通常是非静态(non-stationary)、非独立同分布(non-iid)的,因为一个状态数据可能是持续流入的,而且下一个状态通常与前一个状态是高度相关的。因此,我们需要一个适用于非静态、非独立同分布的数据的训练方法来得到近似函数。
接下来将介绍两种价值函数的近似方法:增量方法和批量方法,这两种方法分别与机器学习中的随机梯度下降和批量梯度下降相对应,主要思想都是梯度下降。
增量方法(Incremental Methods)
梯度下降与随机梯度下降
设 $J(\pmb w)$ 是关于参数向量 $\pmb w$ 的可微函数,那么 $J(\pmb w)$ 的梯度为
梯度代表函数变化最大的方向,为了找到 $J(\pmb w)$ 的局部最小点,可以沿着梯度相反的方向调整 $\pmb w$:
其中 $\alpha$ 是步长参数,也称为学习率参数。
在实际问题中,常常使用随机梯度下降(SGD),因为它不仅可以节省计算时间,还可以避免陷入局部极值,收敛到全局极值。
对于形如 $\displaystyle F(x)=\dfrac{1}{n}\sum_{i=1}^nF_i(x)$ 的目标函数,按梯度下降法的迭代公式为
而按照随机梯度下降法的迭代公式则为
这里的 $i$ 随机选自 ${1,2,\dots,n}$。
利用随机梯度下降法估计值函数的目标是寻找一个参数向量 $\pmb w$ 使得估计值 $\hat{v}(s,\pmb w)$ 和真实值 $v_\pi(s)$ 之间的均方误差最小,即
-
梯度下降能够找到局部最小值:
$\Delta\pmb w=\alpha\mathbb E_\pi[(v_\pi(s)-\hat{v}(s,\pmb w))\nabla_{\pmb w}\hat{v}(s,\pmb w)];$ -
随机梯度下降对梯度进行更新来近似差的期望:
$\Delta\pmb w=\alpha(v_\pi(s)-\hat{v}(s,\pmb w))\nabla_{\pmb w}\hat{v}(s,\pmb w).$
线性函数近似
将状态 $s$ 表示为一个特征向量
其中 $x(s)$ 的分量 $x_i(s)$ 是函数 $x_i:\mathcal S\rightarrow\mathbb R$ 的值,称之为状态 $s$ 的一个特征,如:机器人离路标的距离、股市的趋势。
这样,用线性特征表示值函数
于是对于线性模型,使用随机梯度下降的参数更新规则为:
即:参数更新量 $=$ 步长 $\times$ 预测误差 $\times$ 特征值。
下面介绍一种特殊的特征:查表特征(Table Lookup Features)。它将每一个状态看成一个特征,个体具体处在某一个状态时,该状态特征取1,其余取0。参数的数目就是状态数,也就是每一个状态特征有一个参数,即
这样参数向量 $\pmb w$ 本质上相当于给每个状态对应的值函数:
增量预测(Prediction)算法
在之前的公式中都涉及到了值函数的真值 $v_\pi(s)$,而在强化学习中只有即时奖励,没有监督数据,我们需要找到能代替 $v_\pi(s)$ 的目标值,以便使用监督学习的算法学习近似函数的参数。
MC-值函数近似
对于MC,$v_\pi(s)$ 目标为回报 $G_t$:
回报 $G_t$ 是真实值 $v_\pi(s_t)$ 的有噪声、无偏(高方差)采样,可以把它看成是监督学习的标签数据代入机器学习算法进行学习,训练数据集为
如果使用线性蒙特卡洛估计,那么每次参数的修正值为
线性蒙特卡洛估计方法可以收敛至一个局部最优解。

TD(0)-值函数近似
对于 TD(0),$v_\pi(s)$ 目标为TD目标 $R_{t+1}+\gamma\hat{v}(s_{t+1},\pmb w)$:
TD目标 $R_{t+1}+\gamma\hat{v}(s_{t+1},\pmb w)$ 是真实值 $v_\pi(s_t)$ 的有偏估计,但仍可把 $R_{t+1}+\gamma\hat{v}(s_{t+1},\pmb w)$ 当作监督学习中的标签数据进行学习,训练数据集为
如果使用线性 TD(0) 学习,那么每次参数的修正值为
线性 TD(0) 近似收敛至全局最优解。

TD($\pmb\lambda$)-值函数近似
对于 TD($\lambda$),$v_\pi(s)$ 目标为 $\lambda$-回报 $G_t^\lambda$:
$\lambda$-回报 $G_t^\lambda$ 也是真实值 $v_\pi(s)$ 的有偏估计,但也仍可把 $G_t^\lambda$ 当作监督学习中的标签数据进行学习,训练数据集为
如果使用前向线性 TD($\lambda$) 学习,那么每次参数的修正值为
如果使用后向线性 TD($\lambda$) 学习,那么每次参数的修正值为
其中 $\delta_t=R_{t+1}+\gamma\hat{v}(s_{t+1},\pmb w)-\hat{v}(s_t,\pmb w)$,$E_t=\gamma\lambda E_{t-1}+x(s_t)$。
同样地,前向线性 TD($\lambda$) 和后向线性 TD($\lambda$) 是等价的。此外,线性 TD($\lambda$) 近似收敛至全局最优解。
增量控制(Control)算法
将近似值函数引入到控制过程中需要能够近似行动值函数而不是仅针对状态值函数进行近似。
- 策略估计:用估计方法计算行动值函数的值 $\hat{q}(s,a,\pmb w)\approx q_\pi(s,a)$;
- 策略提升:仍用之前的 $\varepsilon$-贪婪算法。
同样地,我们的目标是寻找一个参数向量 $\pmb w$ 使得估计值 $\hat{q}(s,a,\pmb w)$ 和真实值 $q_\pi(s,a)$ 之间的均方误差最小,即
利用随机梯度下降去寻找最优值:
将状态 $s$ 和动作 $a$ 表示为一个特征向量
那么行动值函数可以表示为
于是对于线性模型,使用随机梯度下降的参数更新规则为:
跟之前的预测部分一样,我们需要用目标来代替未知的 $q_\pi(s,a)$。
-
MC:
$\Delta\pmb w=\alpha(G_t-\hat{q}(s_t,a_t,\pmb w))\nabla_{\pmb w}\hat{q}(s_t,a_t,\pmb w).$ -
TD(0):
$\Delta\pmb w=\alpha(R_{t+1}+\gamma\hat{q}(s_{t+1},a_{t+1},\pmb w)-\hat{q}(s_t,a_t,\pmb w))\nabla_{\pmb w}\hat{q}(s_t,a_t,\pmb w).$ -
前向 TD($\lambda$):
$\Delta\pmb w=\alpha(q_t^\lambda-\hat{q}(s_t,a_t,\pmb w))\nabla_{\pmb w}\hat{q}(s_t,a_t,\pmb w).$ -
后向 TD($\lambda$):
$\Delta\pmb w=\alpha\delta_tE_t,$ 其中 $\delta_t=R_{t+1}+\gamma\hat{q}(s_{t+1},a_{t+1},\pmb w)-\hat{q}(s_t,a_t,\pmb w)$,$E_t=\gamma\lambda E_{t-1}+\nabla_{\pmb w}\hat{q}(s,a,\pmb w).$

预测算法和控制算法的收敛性
预测算法的收敛性
下表给出各种算法在使用不同近似函数进行预测学习时是否收敛的小结。
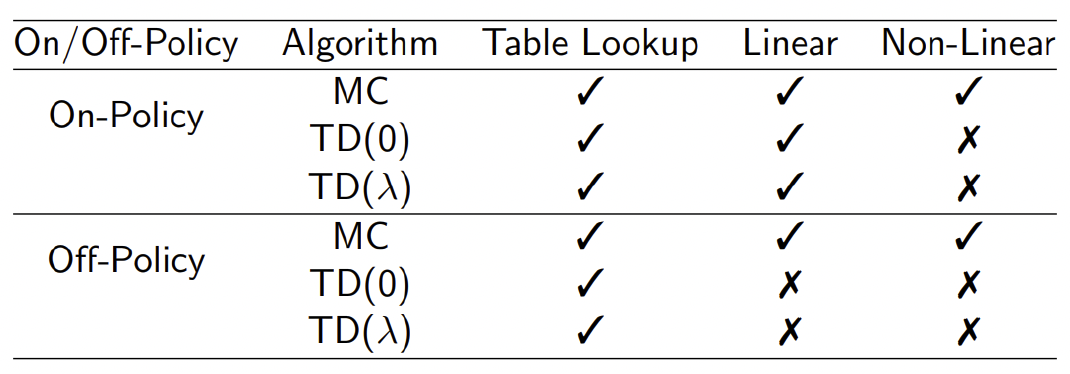
MC使用的是实际价值的有噪声无偏估计,虽然很多时候表现很差,但总能收敛至局部或全局最优解。TD性能通常表现得更好,但TD并不是一直收敛的。而MC算法在实际中是很少使用的,这给强化学习的实际应用带来一定的挑战。好在我们有一些改善TD算法的办法。
梯度时序差分学习(Gradient Temporal-Difference Learning)
TD算法在更新参数时不遵循任何目标函数的梯度是导致它在异策略或使用非线性近似函数可能会发散的原因,我们可以通过修改TD算法使得它遵循投影贝尔曼误差的梯度进而收敛。
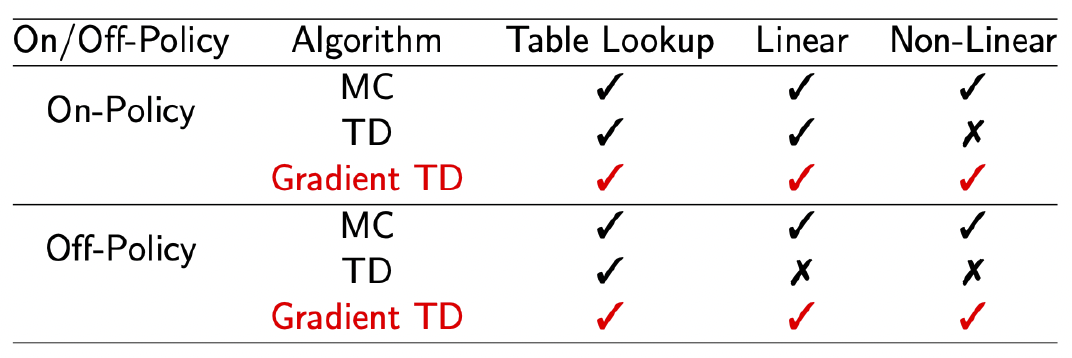
控制算法的收敛性
下表给出各种算法在使用不同近似函数进行控制学习时是否收敛的小结。
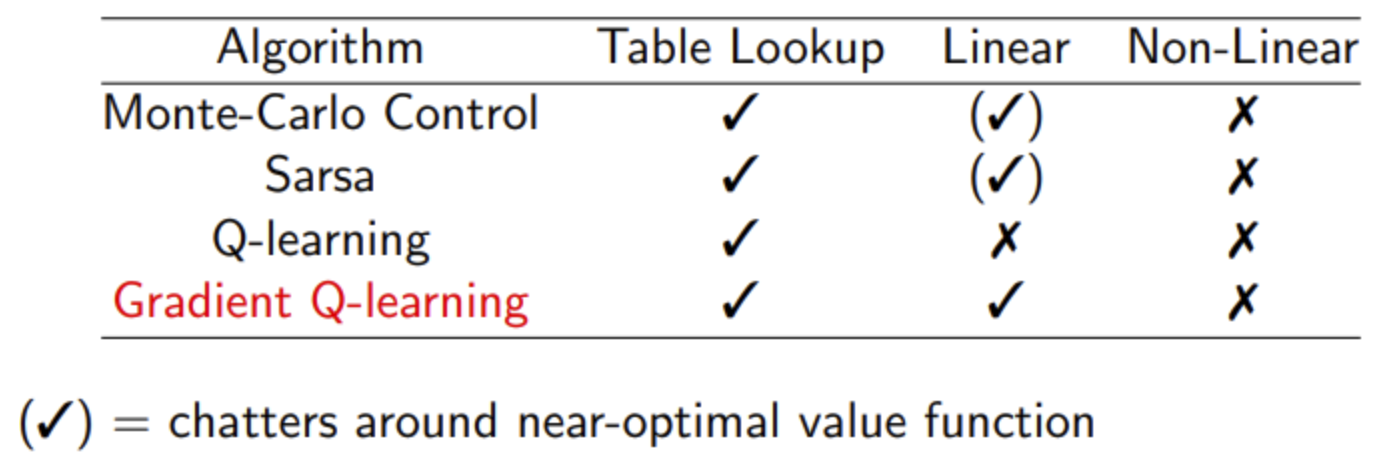
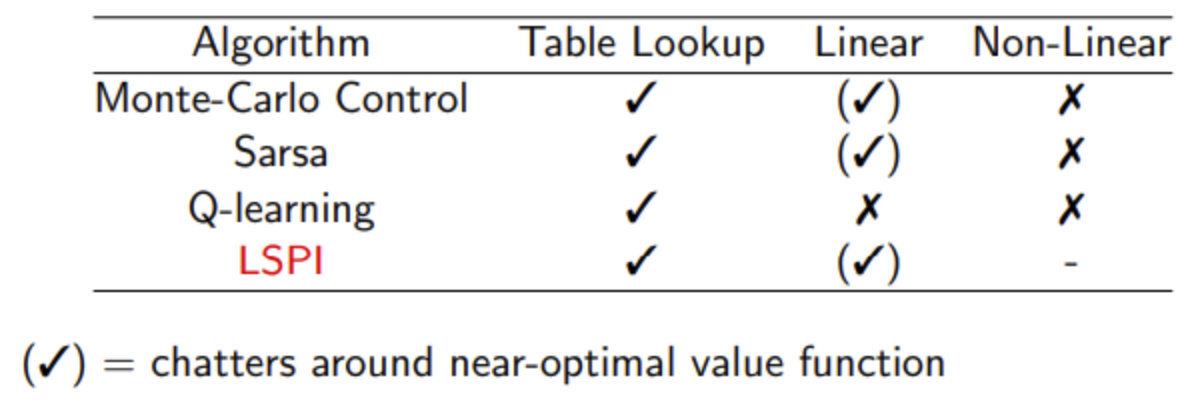
针对控制算法,大多数都能得到较好的策略,但是理论上只要存在函数近似,就都不是严格收敛的,比较常见的是在最优策略上下震荡,逐渐逼近然后突然来一次发散,再逐渐逼近等。而且使用非线性函数近似的效果要比线性函数要差很多。
批量方法(Batch Methods)
增量方法简单且有效,但是不能很有效地利用样本数据,因为这种递增算法再更新后,就不再使用这步的数据,有时不够高效。批量方法则希望找到一个更好的数据拟合方法,它把一段时期内的数据集中起来,通过学习来使得参数能较好地符合这段时期内的所有数据。
最小二乘预测
假设存在一个值函数的近似 $\hat{v}(s,\pmb w)\approx v_\pi(s)$ 以及一段时期内的包含 <状态,价值> 的经历 $D$:
最小二乘法通过最小化 $\hat{v}(s_t,\pmb w)$ 和真实值 $v_t^\pi$ 之间的误差平方和,从而得到参数 $\pmb w$,即
采用经历重现的随机梯度下降来更新参数:
- 从经历 $D$ 中采样一个 $\langle s,v^\pi\rangle\sim D$;
-
应用随机梯度下降来更新参数:
$\Delta\pmb w=\alpha(v^\pi-\hat{v}(s,\pmb w))\nabla_{\pmb w}\hat{v}(s,\pmb w).$
这样得到的最终结果将收敛到针对这段经历的最小二乘估计 $\pmb w^\pi=\underset{\pmb w}{\arg\min}~LS(\pmb w)$。
线性最小二乘预测
一般来说,经历重现可以得到最小二乘估计,但它需要多次迭代。我们可以设计一个值函数的线性近似函数:
于是,利用最小二乘估计的计算方式,可得
如果状态 $s$ 有 $N$ 个特征,直接求解的时间复杂度是 $O(N^3)$,使用Shermann-Morrison法求解复杂度是 $O(N^2)$。这意味着求解该问题的难度与设计的特征数量多少有关,而与状态空间大小无关,因此直接求解适合应用于那些特征较少的问题。
然而,同样的问题是,我们在实际应用中并不知道 $v_t^\pi$ 的真实值。
-
LSMC:$v_t^\pi\approx G_t$,则
$\displaystyle\pmb w=\left[\sum_{t=1}^Tx(s_t)x(s_t)^\textsf{T}\right]^{-1}\sum_{t=1}^Tx(s_t)G_t.$ -
LSTD:$v_t^\pi\approx R_{t+1}+\gamma\hat{v}(s_{t+1},\pmb w)=R_{t+1}+\gamma x(s_{t+1})^\textsf{T}\pmb w$,则
$\displaystyle\pmb w=\left[\sum_{t=1}^Tx(s_t)(x(s_t)-\gamma x(s_{t+1}))^\textsf{T}\right]^{-1}\sum_{t=1}^Tx(s_t)R_{t+1}.$ -
LSTD($\lambda$):前向 $v_t^\pi\approx G_t^\lambda$,则(后向)
$\displaystyle\pmb w=\left[\sum_{t=1}^TE_t(x(s_t)-\gamma x(s_{t+1}))^\textsf{T}\right]^{-1}\sum_{t=1}^TE_tR_{t+1}.$
下表给出了线性最小二乘预测算法的收敛性。
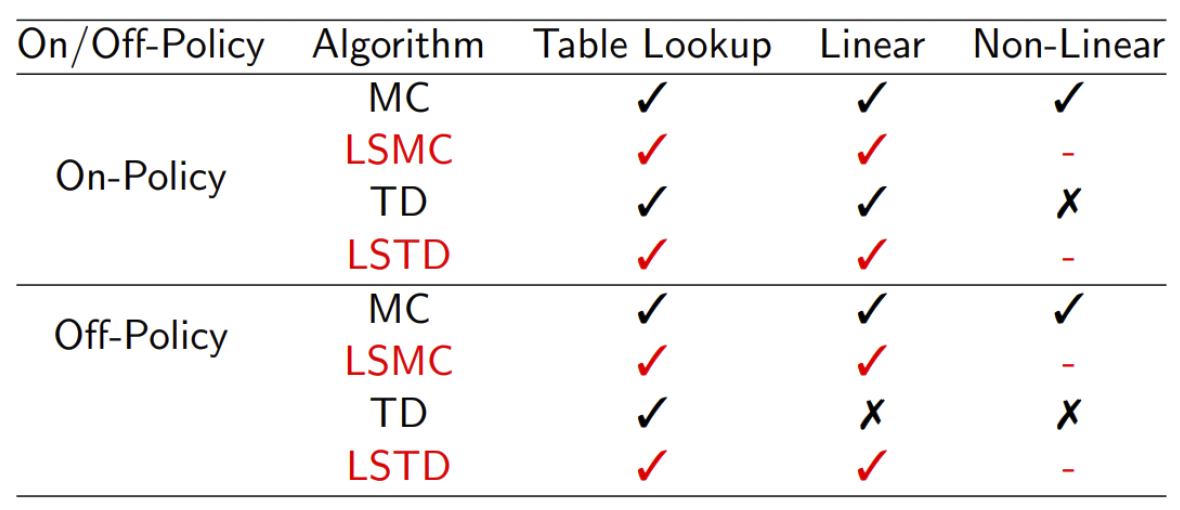
最小二乘控制
将近似值函数引入到控制过程中需要能够近似行动值函数而不是仅针对状态值函数进行近似。
- 策略评估:用最小二乘Q-Learning做策略评估;
- 策略提升:采用贪婪算法。
针对行动值函数的线性近似为
对于用策略 $\pi$ 生成的样本数据
用最小二乘法最小化 $\hat{q}(s,a,\pmb w)$ 与 $q_\pi(s,a)$ 之间的误差。
对于策略评估,我们想要有效地利用所有的经历。对于策略控制,我们同样想要改善策略。这些经历由很多策略生成,因此,为了评估 $q_\pi(s,a)$,我们必须使用off-policy学习。我们使用和Q-学习相同的思想:
- 用旧的策略生成样本 $S_t,A_t,R_{t+1},S_{t+1}\sim\pi_{\text{old}}$;
- 用新的策略选择不同的后继动作 $A’=\pi_{\text{new}}(S_{t+1})$;
- 用 $R_{t+1}+\gamma\hat{q}(S_{t+1},A’,\pmb w)$ 更新 $\hat{q}(S_t,A_t,\pmb w)$。
考虑下面的线性Q-Learning更新
LSTDQ算法的参数计算结果为
下表给出了控制算法的收敛性。
后记
本文内容来自中国科学技术大学《强化学习》(2022Fall)课件。
如对本文内容有任何疑问,请联系 watthu@mail.ustc.edu.cn。