RL-Lec7 策略梯度

介绍

在值函数估计中，我们介绍了如何对值函数进行近似的参数化表达，进而根据这个值函数来产生策略，选择行动。而在本节中，我们将直接参数化策略本身。所谓参数化的策略，指我们用 $\theta$ 作为策略的参数向量，即

$\pi_\theta(s,a)=\mathbb P(A_t=a\mid S_t=s,\theta).$

策略梯度直接对策略进行建模，然后进行优化，得到最优策略，具体的机制是设计一个目标函数，对其使用梯度上升（Gradient Ascent）算法优化参数以最大化奖励。

Softmax策略

Softmax策略是针对离散的行为常用的一个策略。我们希望有平滑的参数化的策略来决策：针对每一个离散的行为，应该以什么样的概率来执行它。

给定 $(s,a)$ 有相应的线性特征 $\phi(s,a)$，$\theta$ 为相应的权重：

$h(s,a,\theta)=\phi(s,a)^\textsf{T}\theta=\left(\phi_1(s,a),\phi_2(s,a),\dots,\phi_n(s,a)\right)^\textsf{T}\theta.$

我们采取某一具体行为的概率与 $\text{e}$ 的该值次幂成正比，即

$\pi_\theta(s,a)=\dfrac{\exp(h(s,a,\theta))}{\sum_b\exp(h(s,b,\theta))}=\dfrac{\exp(\phi(s,a)^\textsf{T}\theta)}{\sum_b\exp(\phi(s,b)^\textsf{T}\theta)}.$

Gaussian策略

与Softmax策略不同，Gaussian策略常应用于连续行为空间。使用Gaussian策略时，通常对于均值有一个参数化的表示，同样可以是一些特征的线性代数和：

$\mu(s)=\phi(s)^\textsf{T}\theta.$

而方差可以是固定值，也可以用参数化表示。这时行动 $a\sim N(\mu(s),\sigma^2)$ 的概率密度为

$\pi_\theta(s,a)=\dfrac{1}{\sqrt{2\pi\sigma^2}}\exp\left(-\dfrac{(a-\mu(s))^2}{2\sigma^2}\right).$

基于策略学习的优点与缺点

优点：
- 基于策略的学习可能会具有更好的收敛性，这是因为基于策略的学习虽然每次只改善一点点，但总是朝着好的方向在改善。
- 在对于那些拥有高维度或连续行动空间来说，使用基于价值函数的学习在得到价值函数后，制定策略时，需要比较各种行为对应的价值大小，这样如果行为空间维度较高或者是连续的，则从中比较得出一个有最大价值函数的行为这个过程就比较难了，这时候使用基于策略的学习就高效的多。
- 能够学到一些随机策略，而基于价值函数的学习通常是学不到随机策略的。
- 有时候计算价值函数非常复杂。
缺点：
- 通常收敛到局部最优而不是全局最优。
- 原始（Naive）的基于策略的学习有时候效率不高，有时候还有较高的方差。

基于策略的强化学习目标函数

基于策略的强化学习的目标是，在给定带参数 $\theta$ 的策略 $\pi_\theta(s,a)$ 下找到最优的 $\theta$。设 $\tau=(S_t,A_t,R_{t+1},S_{t+1},A_{t+1},\dots)$ 为一回合，其总回报为

$\displaystyle r(\tau)=R_{t+1}+\gamma R_{t+2}+\cdots=\sum_{k=0}^{\infty}\gamma^kR_{t+k+1}.$

记 $\pi_\theta(\tau)$ 为给定策略 $\pi_\theta$ 下，经历 $\tau$ 的概率分布，则评价策略的直观解释是最大化目标函数

$J(\theta)=\mathbb E_{\tau\sim\pi_\theta(\tau)}[r(\tau)].$

针对不同的问题类型，有三种具体的目标函数可以选择：

初始值：在能够产生完整回合的环境下，从某状态 $s_1$ 算起直到终止状态个体获得的累积奖励可以用来衡量整个策略的优劣：
$J_1(\theta)=V^{\pi_\theta}(s_1)=\mathbb E_{\tau\sim\pi_\theta(\tau)}[r(\tau)\mid S_t(\tau)=s_1].$
平均值：对于连续环境条件，不存在一个开始状态，可以使用平均值。考虑某时刻的状态分布及以每个可能的状态开始一直持续与环境交互下去能够得到的奖励的概率加权和来衡量整个策略的优劣：
$\displaystyle J_{\text{avV}}(\theta)=\sum_sd^{\pi_\theta}(s)V^{\pi_\theta}(s),$
其中 $d^{\pi_\theta}(s)$ 是在当前策略下马尔科夫链的静态分布。
每步平均奖励：在连续环境条件下，也可以在每个时间步在各种情况下求平均奖励。在一个确定的时间步长里，查看个体处于所有状态的可能性，按每一种状态下采取所有行为能够得到的即使奖励按概率加权和来衡量整个策略的优劣：
$\displaystyle J_{\text{avR}}(\theta)=\sum_sd^{\pi_\theta}(s)\sum_a\pi_\theta(s,a)\mathcal R_s^a,$
其中 $\mathcal R_s^a=\mathbb E(R_{t+1}\mid S_t=s,A_t=a)$，$d^{\pi_\theta}(s)$ 是在当前策略下马尔科夫链的静态分布。

基于策略优化的强化学习本质上就是优化问题，需要找到使得目标函数 $J(\theta)$ 最大的 $\theta$。一般有无梯度方法（爬山法、模拟退火法、遗传算法）和梯度方法（梯度下降法、共轭梯度法、牛顿法、拟牛顿法）来实现优化。

下面我们将聚焦于梯度下降方法，同时使用基于序列结构片段（Sequential Structure）的方法。

有限差分策略梯度

令 $J(\theta)$ 为任何类型的策略目标函数，策略梯度算法可以使 $J(\theta)$ 沿着其梯度

$\nabla_\theta J(\theta)=\left(\dfrac{\partial J(\theta)}{\partial\theta_1},\dfrac{\partial J(\theta)}{\partial\theta_2},\dots,\dfrac{\partial J(\theta)}{\partial\theta_n}\right)^\textsf{T}$

上升至局部最大值，参数更新方式如下：

$\theta\leftarrow\theta+\Delta\theta=\theta+\alpha\nabla_\theta J(\theta).$

给定策略 $\pi_\theta(s,a)$，当 $J(\theta)$ 不可微时，可以采用有限差分法计算梯度：

$\dfrac{\partial J(\theta)}{\partial\theta_k}\approx\dfrac{J(\theta+\varepsilon u_k)-J(\theta)}{\varepsilon},$

其中 $u_k$ 是单位向量，其仅在第 $k$ 维上值为1，其余分量上值为0。

有限差分法较为简单，不要求策略函数可微分，适用于任意策略；但这种方法有噪声，且大多数时候不高效。

策略梯度定理

注意到

$\nabla_\theta\pi_\theta(\tau)=\pi_\theta(\tau)\dfrac{\nabla_\theta\pi_\theta(\tau)}{\pi_\theta(\tau)}=\pi_\theta(\tau)\nabla_\theta\log\pi_\theta(\tau),$

因此策略梯度

$\displaystyle\nabla_\theta J(\theta)=\int\nabla_\theta\pi_\theta(\tau)r(\tau)\text{d}\tau=\mathbb E_{\tau\sim\pi_\theta(\tau)}[\nabla_\theta\log\pi_\theta(\tau)r(\tau)].$

而由 $\pi_\theta(\tau)$ 的定义为

$\begin{array}{rl} \pi_\theta(\tau)=&\!\!\!\!\pi_\theta(S_t,A_t,R_{t+1},\dots,S_T,A_T)\\ =&\!\!\!\!\displaystyle\mathbb P(S_t)\prod_{k=t}^T\pi_\theta(A_k\mid S_k)\mathbb P(S_{k+1}\mid S_k,A_k). \end{array}$

于是

$\begin{array}{rl} \nabla_\theta\log\pi_\theta(\tau)=&\!\!\!\!\displaystyle\nabla_\theta\left[\log\mathbb P(S_t)+\sum_{k=t}^T\log\pi_\theta(A_k\mid S_k)+\sum_{k=t}^T\log\mathbb P(S_{k+1}\mid S_k,A_k)\right]\\ =&\!\!\!\!\displaystyle\sum_{k=t}^T\nabla_\theta\log\pi_\theta(A_k\mid S_k). \end{array}$

所以

$\begin{array}{rl} \nabla_\theta J(\theta)=&\!\!\!\!\mathbb E_{\tau\sim\pi_\theta(\tau)}[\nabla_\theta\log\pi_\theta(\tau)r(\tau)]\\ =&\!\!\!\!\displaystyle\mathbb E_{\tau\sim\pi_\theta(\tau)}\left[\bigg(\sum_{k=t}^T\nabla_\theta\log\pi_\theta(A_k\mid S_k)\bigg)r(\tau)\right]\\ \approx&\!\!\!\!\displaystyle\dfrac{1}{N}\sum_{i=1}^N\left(\sum_{k=t_i}^{T_i}\nabla_\theta\log\pi_\theta(A_k^i\mid S_k^i)\right)\left(\sum_{k=t_i}^{T_i}R(S_k^i,A_k^i)\right)\\ \approx&\!\!\!\!\displaystyle\dfrac{1}{N}\sum_{i=1}^N\left(\sum_{k=t_i}^{T_i}\nabla_\theta\log\pi_\theta(A_k^i\mid S_k^i)\left(\sum_{k'=k}^{T_i}R(S_{k'}^i,A_{k'}^i)\right)\right)\\ \approx&\!\!\!\!\displaystyle\dfrac{1}{N}\sum_{i=1}^N\left(\sum_{k=t_i}^{T_i}\nabla_\theta\log\pi_\theta(A_k^i\mid S_k^i)\left(\sum_{k'=k}^{T_i}\gamma^{k'-k}R(S_{k'}^i,A_{k'}^i)\right)\right). \end{array}$

注意这里最后用到了因果性，即过去影响将来，但将来不会影响过去，从而减小了策略梯度的方差。

下面考虑一步MDP，即从一个分布 $d(s)$ 中采样得到一个状态 $s$，从 $s$ 开始，采取一个行动 $a$，得到即时奖励 $r=\mathcal R_s^a$ 然后终止，此时

$\displaystyle J(\theta)=\sum_sd(s)\sum_a\pi_\theta(s,a)\mathcal R_s^a.$

相应梯度为

$\displaystyle\nabla_\theta J(\theta)=\sum_sd(s)\sum_a\pi_\theta(s,a)\nabla_\theta\log\pi_\theta(s,a)\mathcal R_s^a=\mathbb E_{\pi_\theta}[\nabla_\theta\log\pi_\theta(s,a)\mathcal R_s^a].$

对于多步MDP，只需要将 $\mathcal R_s^a$ 替换为 $q^{\pi_\theta}(s,a)$ 即可。

定理(策略梯度定理) 对于任何可微策略 $\pi_\theta(s,a)$，对于任何目标策略函数 $J=J_1$，$J_{\text{avR}}$ 或 $\dfrac{1}{1-\gamma}J_{\text{avV}}$，策略梯度为

$\displaystyle\nabla_\theta J(\theta)=\mathbb E_{\pi_\theta}[\nabla_\theta\log\pi_\theta(s,a)q^{\pi_\theta}(s,a)].$

在上式中，对数梯度部分可以看作是采取某个行动的方向，而后一部分可以看作是采取这个行动的奖励。例如，对于Softmax策略，

$\nabla_\theta\log\pi_\theta(s,a)=\phi(s,a)-\dfrac{\sum_b\exp(\phi(s,b)^\textsf{T}\theta)\phi(s,b)}{\sum_b\exp(\phi(s,b)^\textsf{T}\theta)}=\phi(s,a)-\mathbb E_{\pi_\theta}[\phi(s,\cdot)].$

对于Gaussian策略，

$\nabla_\theta\log\pi_\theta(s,a)=\dfrac{(a-\mu(s))\phi(s)}{\sigma^2}.$

蒙特卡洛策略梯度

针对具有完整回合的情况，基于策略梯度定理，我们可以构建第一个策略梯度算法——REINFORCE（Williams，1992）。REINFORCE通过蒙特卡洛的方法来估计回报，所以又称为蒙特卡洛策略梯度。具体来说，策略梯度为

$\nabla_\theta J(\theta)=\mathbb E_{\pi_\theta}[\nabla_\theta\log\pi_\theta(S_t,A_t)G_t]$

而采用随机梯度下降更新 $\theta$：

$\theta_{t+1}=\theta_t+\alpha G_t\nabla_\theta\log\pi_\theta(S_t,A_t).$

注意到算法中引入了参数 $\gamma$，这是自然的。

Actor-Critic策略梯度

蒙特卡洛策略梯度方法使用了收获作为状态价值的估计，它虽然是无偏低，但是方差较高。除了学习策略之外，学习价值函数也是很有意义，这就导出了Actor-Critic策略梯度算法。

用Critic相对准确地估计状态价值 $q_{\pmb w}(s,a)\approx q^{\pi_\theta}(s,a)$，用它来指导策略更新。由此，Actor-Critic算法维护两组参数：

Critic：参数化行动值函数 $q_{\pmb w}(s,a)$；
Actor：按照Critic部分得到的价值引导策略函数参数 $\theta$ 的更新。

因此，Actor-Critic算法遵循的是一个近似的策略梯度：

$\nabla_\theta J(\theta)\approx\mathbb E_{\pi_\theta}[\nabla_\theta\log\pi_\theta(s,a)q_{\pmb w}(s,a)].$

关于Critic所做的事情，之前已经介绍了许多方法：蒙特卡洛策略评估、TD 学习及 TD($\lambda$)，还可以用最小二乘策略评估等等。

Action-Value Actor-Critic算法

一个简单的Actor-Critic算法可以使用基于行动值函数的Critic，它用一个线性值函数来近似行动值函数：

$q_{\pmb w}(s,a)=\phi(s,a)^\textsf{T}\pmb w,$

其中Critic通过线性近似的TD(0)更新 $\pmb w$，Actor通过策略梯度更新 $\theta$。

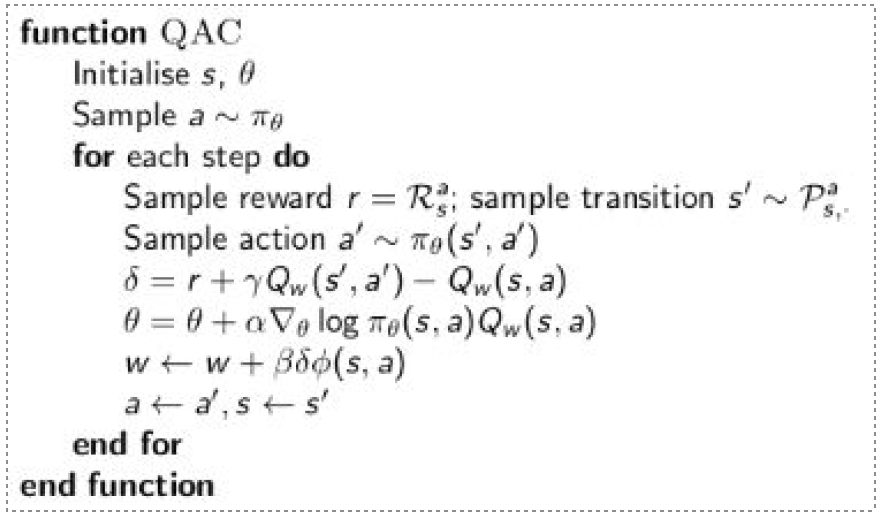
用特征的线性组合来近似动作价值函数引入了偏差，而一个有偏差的策略梯度不一定能找到正确的解。不过，如果我们小心地选择近似的价值函数，可以避免引入任何偏差，这样相当于我们仍然遵循准确的策略梯度。

兼容近似函数

如何才算是一个小心设计的行动值函数呢？一般需要满足下面两个条件：

近似值函数的梯度完全等同于策略函数对数的梯度，即不存在重名情况：
$\nabla_{\pmb w}q_{\pmb w}(s,a)=\nabla_\theta\log\pi_\theta(s,a).$
行动值函数参数 $\pmb w$ 使得均方误差最小：
$\nabla_{\pmb w}\mathbb E_{\pi_\theta}[(q^{\pi_\theta}(s,a)-q_{\pmb w}(s,a))^2]=0.$

符合这两个条件，就认为策略梯度是准确的，此时：

$\nabla_\theta J(\theta)=\mathbb E_{\pi_\theta}[\nabla_\theta\log\pi_\theta(s,a)q_{\pmb w}(s,a)].$

使用基线减小方差

这一方法的基本思想是从策略梯度里抽出一个基准函数 $B(s)$，要求这一函数仅与状态有关，与行动无关，因而不改变梯度本身。$B(s)$ 的特点是能在不改变行为价值期望的同时降低方差。事实上，

$\displaystyle\mathbb E_{\pi_\theta}[\nabla_\theta\log\pi_\theta(s,a)B(s)]=\sum_sd^{\pi_\theta}(s)B(s)\nabla_\theta\sum_a\pi_\theta(s,a)=0.$

原则上，和行为无关的函数都可以作为基准函数，不过一个很好的选择就是基于当前状态的状态值函数 $v^{\pi_\theta}(s)$，由此策略梯度改写为

$\nabla_\theta J(\theta)=\mathbb E_{\pi_\theta}[\nabla_\theta\log\pi_\theta(s,a)(G_t-v_{\pmb w}(s))]$

优势函数及其估计

由上面这种方法，我们考虑引入优势函数的概念，它定义为

$A^{\pi_\theta}(s,a)=q^{\pi_\theta}(s,a)-v^{\pi_\theta}(s).$

优势函数衡量了从状态 $s_t$ 开始，动作 $a_t$ 比平均动作好多少。

优势函数可以明显减少状态价值的变异性，因此算法的Critic部分可以去估计优势函数而不是仅仅估计行动值函数。在这种情况下，我们需要两个近似函数，也就是两套参数来计算优势函数，从而通过TD学习来更新这两个价值函数。即

$v_{\pmb w_1}(s)\approx v^{\pi_\theta}(s),~q_{\pmb w_2}(s,a)\approx q^{\pi_\theta}(s,a),\quad\Rightarrow A(s,a)=q_{\pmb w_2}(s,a)-v_{\pmb w_1}(s).$

不过在实际操作时，并不需要这么做，有简化方式。

根据定义，TD误差 $\delta^{\pi_\theta}$ 可以根据真实的状态值函数算出：

$\delta^{\pi_\theta}=r+\gamma v^{\pi_\theta}(s')-v^{\pi_\theta}(s).$

这个TD误差是优势函数的无偏估计，事实上，

$\begin{array}{rl} \mathbb E_{\pi_\theta}[\delta^{\pi_\theta}\mid s,a]=&\!\!\!\!\mathbb E_{\pi_\theta}[r+\gamma v^{\pi_\theta}(s')\mid s,a]-v^{\pi_\theta}(s)\\ =&\!\!\!\!q^{\pi_\theta}(s,a)-v^{\pi_\theta}(s)=A^{\pi_\theta}(s,a). \end{array}$

因此，就可以使用TD误差来计算策略梯度：

$\nabla_\theta J(\theta)=\mathbb E_{\pi_\theta}[\nabla_\theta\log\pi_\theta(s,a)\delta^{\pi_\theta}].$

而实际运用时则使用一个近似的TD误差

$\delta_{\pmb w}=r+\gamma v_{\pmb w}(s')-v_{\pmb w}(s),$

其中只有一套参数 $\pmb w$。

TD($\lambda$)的Actor-Critic算法

针对Critic过程，通过计算不同时间范围内的TD误差来更新状态值函数 $v_{\pmb w}(s)$：

MC：直至回合结束，更新公式为 $\Delta\pmb w=\alpha(G_t-v_{\pmb w}(s))\phi(s)$.
TD(0)：一步，更新公式为 $\Delta\pmb w=\alpha(r+\gamma v_{\pmb w}(s’)-v_{\pmb w}(s))\phi(s)$.
前向 TD($\lambda$)：需要直至回合结束，更新公式为 $\Delta\pmb w=\alpha(G_t^\lambda-v_{\pmb w}(s))\phi(s)$.
后向 TD($\lambda$)：实时，具备频率记忆和近时记忆功能，更新公式为
$\begin{array}{rl} \delta_t=&\!\!\!\!r_{t+1}+\gamma v_{\pmb w}(s_{t+1})-v_{\pmb w}(s_t),\\ e_t=&\!\!\!\!\gamma\lambda e_{t-1}+\phi(s_t),\\ \Delta\pmb w=&\!\!\!\!\alpha\delta_te_t. \end{array}$

针对Actor过程，也可以把时间范围考虑进去以更新参数。

MC：直至回合结束，更新公式为 $\Delta\theta=\alpha(G_t-v_{\pmb w}(s_t))\nabla_\theta\log\pi_\theta(s_t,a_t)$.
TD(0)：一步，更新公式为 $\Delta\theta=\alpha(r+\gamma v_{\pmb w}(s_{t+1})-v_{\pmb w}(s_t))\nabla_\theta\log\pi_\theta(s_t,a_t)$.
前向 TD($\lambda$)：需要直至回合结束，更新公式为 $\Delta\theta=\alpha(G_t^\lambda-v_{\pmb w}(s_t))\nabla_\theta\log\pi_\theta(s_t,a_t)$.
后向 TD($\lambda$)：实时，具备频率记忆和近时记忆功能，更新公式为
$\begin{array}{rl} \delta_t=&\!\!\!\!r_{t+1}+\gamma v_{\pmb w}(s_{t+1})-v_{\pmb w}(s_t),\\ e_t=&\!\!\!\!\gamma\lambda e_{t-1}+\nabla_\theta\log\pi_\theta(s_t,a_t),\\ \Delta\theta=&\!\!\!\!\alpha\delta_te_t. \end{array}$

后记

本文内容来自中国科学技术大学《强化学习》（2022Fall）课件。

如对本文内容有任何疑问，请联系 watthu@mail.ustc.edu.cn。

Policy Gradient

介绍