Bayes-Lec7 贝叶斯近似推断

后验分布的极限

当样本量 $n\rightarrow\infty$ 时，后验分布的极限行为是我们所关心的。

可以利用后验分布的极限分布进行推断，避免可能是后验导出和先验指定的困难性；
通过对比极限分布下的贝叶斯推断结果和频率方法下的推断结果，验证贝叶斯推断方法的合理性。

后验分布的相合性

对一个合理有效的贝叶斯推断方法而言，随着样本量的增加，感兴趣参数 $\theta$ 的后验信息应该越来越集中在 $\theta_0$ 附近，而越来越少地依赖于先验分布，这种性质即为后验分布在 $\theta_0$ 处的相合性。

考虑一列样本 $D^n,~n=1,2,\dots$，服从模型

$D^n\sim p_n(d^n\mid\theta),~\theta\in\Theta;\quad\theta\sim\Pi_n(\theta),$

记基于第 $n$ 个样本的 $\theta$ 的后验分布函数为 $\Pi_n(\cdot\mid D^n)$：

$\Pi_n(B\mid D^n)=\dfrac{\int_Bp_n(D^n\mid\theta)\text{d}\Pi_n(\theta)}{\int_\Theta p_n(D^n\mid\theta)\text{d}\Pi_n(\theta)},\quad B\subset\Theta.$

如果后验分布在 $\theta_0$ 处有相合性，那么 $\Pi_n(\cdot\mid D^n)$ 应在 $\Theta$ 上弱收敛到一个Dirac测度 $\delta_{\theta_0}$。

为此，记 $\Theta$ 为一个度量空间，$\text{d}_W$ 为其上的一个测度（Levy-Prokhorov或Wasserstein），并定义

$\rho_n(\theta)=\text{d}_W(\Pi_n(\cdot\mid D^n),\delta_\theta),$

其为 $D^n$ 和 $\theta$ 的函数。

定义. 称后验分布 $\Pi_n(\cdot\mid D^n)$ 在 $\theta_0$ 处是（弱）相合的，如果有 $\rho_n(\theta_0)\overset{\text{a.s.}}\rightarrow0$ 或 $\rho_n(\theta_0)\overset{P}\rightarrow0$.

直接验证 $\text{d}_W$ 是比较困难的，下面引理给出了在额外一些条件下后验相合性的等价描述。

引理. 设度量空间 $(\Theta,\text{d})$ 是可分的，则

$\rho_n(\theta_0)\Longleftrightarrow\Pi_n(U^c\mid D^n)\rightarrow0$ 对 $\theta_0$ 的每个开邻域 $U$.

这里的收敛也是几乎处处收敛或依概率收敛，所有的收敛均在 $\theta=\theta_0$ 处计算。

定理(参数空间可数场合). 设 $X\mid\theta\sim f(\cdot\mid\theta)$，其中 $\theta\in\Theta={\theta_1,\theta_2,\dots}$ 为可数集，并假设 $\theta_t\in\Theta$ 为 $\theta$ 的真值。如果先验分布 $\pi(\theta)$ 满足 $\pi(\theta_i)>0,~i=1,2,\dots$ 以及

$\displaystyle KL(f_{\theta_t}\| f_{\theta_i})=\int f(x\mid\theta_t)\log\dfrac{f(x\mid\theta_t)}{f(x\mid\theta_i)}\text{d}x>0,\quad\forall i\neq t,$

则对样本 $\pmb x=(x_1,\dots,x_n)$ 有

$\lim\limits_{n\rightarrow}\pi(\theta_t\mid\pmb x)=1$ 以及 $\lim\limits_{n\rightarrow\infty}\pi(\theta_i\mid\pmb x)=0,\quad\forall i\neq t.$

注: 如果 $\theta_t\notin\Theta$，则后验分布收敛到一个在K-L距离意义下距离真实模型最近的一个离散分布。

证明: 由贝叶斯公式

$\begin{array}{rl} \pi(\theta_i\mid\pmb x)=&\!\!\!\!\dfrac{\pi(\theta_i)f(\pmb x\mid\theta_i)}{\sum_j\pi(\theta_j)f(\pmb x\mid\theta_j)}\\ =&\!\!\!\!\dfrac{\pi(\theta_i)f(\pmb x\mid\theta_i)/f(\pmb x\mid\theta_t)}{\sum_j\pi(\theta_j)f(\pmb x\mid\theta_j)/f(\pmb x\mid\theta_t)}\\ =&\!\!\!\!\dfrac{\exp(\log\pi(\theta_i)+S_i)}{\sum_j\exp(\log\pi(\theta_j)+S_j)}, \end{array}$

其中 $S_i=\sum\limits_{j=1}^n\log\dfrac{f(x_j\mid\theta_i)}{f(x_j\mid\theta_t)}$。在给定 $\theta_t$ 的条件下，$S_i$ 为i.i.d.随机变量之和，因此由大数定律有

$\displaystyle\lim_{n\rightarrow\infty}\frac{S_i}{n}=\mathbb E_{X\vert\theta_t}\left[\log\dfrac{f(X\mid\theta_i)}{f(X\mid\theta_t)}\right]=\int f(x\mid\theta_t)\log\dfrac{f(x\mid\theta_i)}{f(x\mid\theta_t)}\text{d}x.$

由定理假设知当 $i\neq t$ 时为负，当 $i=t$ 时为0。因此当 $n\rightarrow\infty$ 时，$S_t\rightarrow0$，$S_i\rightarrow-\infty,~i\neq t$，从而定理得证。

定理(参数空间连续场合). 设 $X\mid\theta\sim f(\cdot\mid\theta)$，其中 $\theta\in\Theta$ 为紧集，并假设 $\theta_t\in\Theta$ 为 $\theta$ 的真值。记 $A$ 为 $\theta_t$ 的先验概率非零的任意一个邻域，则对样本 $\pmb x=(x_1,\dots,x_n)$ 有

$\lim\limits_{n\rightarrow\infty}\pi(\theta_t\in A\mid\pmb x)=1.$

注: 这里由于 $\theta$ 取任意值的概率为零，因此定义的是

$\displaystyle\theta_t=\arg\min H(\theta)=\arg\min\int f(x\mid\theta_t)\log\dfrac{f(x\mid\theta_t)}{f(x\mid\theta)}\text{d}x.$

证明: 由于 $\Theta$ 为紧集，故存在有限子覆盖，其中仅有 $A$ 包含 $\theta_t$，于是由离散场合的结论可证。

当后验相合性成立时，有下述两个重要结论。

定理. 设 $\Theta^\star\subset\Theta$ 是使得后验相合性在每个 $\theta_0\in\Theta^\star$ 都成立的子集，则

存在一个估计量 $\hat{\theta}_n=T(D^n)$ 对每个 $\theta_0\in\Theta^\star$ 都相合，即对每个 $\theta_0\in\Theta^\star$，当 $D^n\sim p_n(\cdot\mid\theta_0)$ 时有 $\text{d}(\hat{\theta}_n,\theta_0)\rightarrow0$ 几乎处处/依概率。如果后验分布以速度 $\varepsilon_n$ 压缩到 $\theta_0\in\Theta^\star$，则 $\varepsilon_n^{-1}\text{d}(\hat{\theta}_n,\theta_0)$ 是几乎处处/依概率有界的。
如果 $\Theta$ 是凸集以及 $\text{d}$ 是有界且凸的，则可取 $\hat{\theta}_n$ 为后验均值 $\displaystyle\overline{\theta}_n=\int \theta\text{d}\Pi_n(\theta\mid D^n)$。

和相合性有关的另一重要结果是后验推断对先验分布选择的稳健性——从两个不同先验出发的后验是渐近相同的。

定理. 设在参数空间 $\Theta$ 上对所有 $n$ 使用相同的先验 $\Pi_n\equiv\Pi$，$\Gamma$ 是 $\Theta$ 上不同的一个先验。记 $P_{\Gamma}^{\infty}$ 为样本 $(X_1,X_2,\dots)$ 在模型 $X_i\overset{\text{i.i.d.}}{\sim} f(\cdot\mid\theta),~\theta\sim\Gamma$ 下的边际分布，则

$\text{d}_W(\Pi(\cdot\mid D^n),\Gamma(\cdot\mid D^n))\rightarrow0,\quad\text{a.s.}~P_\Gamma^\infty,$

当且仅当 $\Pi(\cdot\mid D^n)$ 在每个 $\theta\in\text{supp}(\Gamma)$ 几乎处处相合，即

$\rho_n(\theta)\rightarrow0,\quad\text{a.s.}~P_\theta^\infty.$

Schwartz（1965）对i.i.d.样本 $D^n=(X_1,\dots,X_n)\in\mathcal X^n$ 场合提供了后验相合性的一个一般且明显的充分条件，其中 $X_i\overset{\text{i.i.d.}}{\sim}f$，$f\sim\Pi$，这里先验分布 $\Pi$ 是概率密度函数的集合 $\cal F$ 上的一个概率测度，这里取 $\cal X$ 上的Lebesgue测度。令

$\displaystyle\text{d}_{KL}(p,q)=\int p(x)\log\dfrac{p(x)}{q(x)}\text{d}x$

表示K-L散度，$\Phi_n$ 表示 $\mathcal X^n\mapsto[0,1]$ 的任一检验函数。

假设 $f=f_0$ 为真实的密度，令 $P_0^\infty$ 表示 $(X_1,X_2,\dots)$ 在 $f_0$ 下的联合密度。称 $f_0$ 属于 $\Pi$ 的KL支撑，如果对任意 $\varepsilon>0$，

$\Pi(\{f:\text{d}_{KL}(f_0,f)<\varepsilon\})>0.$

定理. 如果 $f_0$ 属于 $\Pi$ 的KL支撑，$U_n\subset\mathcal F$ 为 $f_0$ 的邻集且使得存在检验函数 $\Phi_n,~n=1,2,\dots$ 满足条件

$\mathbb E_{f_0}\Phi_n\leq B\text{e}^{-bn},\quad\sup\limits_{f\in U_n^c}\mathbb E_f(1-\Phi_n)\leq B\text{e}^{-bn},$

其中 $b,B>0$ 为正常数，则 $\Pi(U_n^c\mid D^n)\rightarrow0,~\text{a.s.}~P_0^\infty$。

注: 检验函数 $\Phi_n$ 为在样本 $D^n$ 下假设 $H_0:f=f_0\leftrightarrow H_1:f\in U_n^c$ 的检验函数。

推论. 如果 $f_0$ 属于 $\Pi$ 的KL支撑，则后验分布在 $f_0$ 处弱相合。

当后验分布相合时，可以考虑刻画收敛的速度（或者该速度的界）。

定义. 设 $(\Theta,\text{d})$ 为度量空间，$\theta=\theta_0\in\Theta$ 为真值，样本 $D^n\sim p_n(\cdot\mid\theta_0)$。后验分布 $\Pi_n(\cdot\mid D^n)$ 称为以速度 $\varepsilon_n\rightarrow0$（或更快）在 $\delta_{\theta_0}$ 处收缩，如果对每个 $M_n\rightarrow\infty$，

$\Pi_n(\{\theta:\text{d}(\theta,\theta_0)>M_n\varepsilon_n\mid D^n\})\overset{P}{\rightarrow}0.$

注: 序列 $M_n\rightarrow\infty$ 是为了技术方便性而需要的，在许多问题中 $M_n\equiv M$ 就足够了。

考虑i.i.d.情形，记 $D^n=(X_1,\dots,X_n)$，$X_i\overset{\text{i.i.d.}}{\sim}f(x_i\mid\theta)$。令

$K(\theta_0;\theta)=\text{d}_{KL}(f(\cdot\mid\theta_0),f(\cdot\mid\theta))=\mathbb E_{\theta_0}\left[\log\dfrac{f(X_1\mid\theta_0)}{f(X_1\mid\theta)}\right],\\ V(\theta_0;\theta)=\mathbb E_{\theta_0}\left[\log^2\dfrac{f(X_1\mid\theta_0)}{f(X_1\mid\theta)}\right],$

记 $N(\varepsilon,\mathcal P,\text{d})$ 表示使用半径为 $\varepsilon$ 的 $\text{d}$-球覆盖集合 $\cal P$ 所需要的最小个数，称为是 $\cal P$ 的 $\varepsilon$-覆盖数。

定理. 令 $\varepsilon_n\rightarrow0$ 使得 $n\varepsilon_n^2\rightarrow\infty$，存在集合 $\Theta_n\subset\Theta,n\geq1$ 和常数 $c_1,c_2>$ 满足

$\log N(\varepsilon_n,\Theta_n,\text{d})\leq c_1n\varepsilon_n^2$；
$\Pi(\Theta_n^c)\leq\text{e}^{-(4+c_2)n\varepsilon_n^2}$，

则后验 $\Pi(\cdot\mid D^n)$ 以速度 $\varepsilon_n$ 或者更快在每个满足集中不等式

$\Pi\left(\{\theta:K(\theta_0;\theta)<\varepsilon_n^2,V(\theta_0;\theta)<\varepsilon_n^2\}\right)\geq\text{e}^{-c_2n\varepsilon_n^2}$

的 $\theta_0$ 处收缩。

后验分布的渐近正态性

当样本量 $n$ 增加时，后验分布在一般条件下渐近趋于正态分布，可以被一个合适的正态分布很好地近似。

定理. 在一些正则条件下，后验分布 $\pi(\theta\mid\pmb x)$ 趋于正态分布 $N(\tilde{\theta},\tilde{I}_n^{-1}(\tilde{\theta}))$，其中 $\tilde{\theta}$ 为MAP估计，$\tilde{I}_n(\theta)=-\dfrac{\partial^2\log\pi(\theta\mid\pmb x)}{\partial\theta\partial\theta^\textsf{T}}$ 为样本的Fisher信息阵。

证明: 将对数似然函数在 $\tilde{\theta}$ 处Taylor展开得到

$\log\pi(\theta\mid\pmb x)=\log\pi(\tilde{\theta}\mid\pmb x)-\dfrac{1}{2}(\theta-\tilde{\theta})^\textsf{T}\tilde{I}_n(\tilde{\theta})(\theta-\tilde{\theta})+\cdots.$

在合适的条件下可以证明高阶项可忽略，进而后验密度近似正比于

$\exp\left\{-\dfrac{1}{2}(\theta-\tilde{\theta})^\textsf{T}\tilde{I}_n(\tilde{\theta})(\theta-\tilde{\theta})\right\},$

这是正态密度 $N(\tilde{\theta},\tilde{I}_n^{-1}(\tilde{\theta}))$ 的核。

当后验密度高度集中在后验众数 $\tilde{\theta}$ 的小邻域时，由于先验密度在此小邻域内几乎为常数，因此后验密度 $\pi(\theta\mid\pmb x_n)$ 本质上等于似然函数 $f(\pmb x_n\mid\theta)$。因此，可以使用极大似然估计 $\hat{\theta}_n$ 来代替众数 $\tilde{\theta}$，使用观测到的 $p\times p$ Fisher信息阵

$\hat{I}_n=\left(-\dfrac{\partial^2\log f(\pmb x_n\mid\theta)}{\partial\theta\partial\theta^\textsf{T}}\right)\Bigg\vert_{\theta=\hat{\theta}_n}$

来代替 $\tilde{I}_n$。因此 $\theta$ 的后验分布近似为 $N(\hat{\theta}_n,\hat{I}_n^{-1})$。

此外，$\hat{I}_n$ 也可以使用期望的Fisher信息阵在极大似然估计 $\hat{\theta}_n$ 处的值来代替，即使用 $p\times p$ 矩阵

$I(\theta)=\mathbb E\left[-\dfrac{\partial^2\ln f(\pmb x_n\mid\theta)}{\partial\theta\partial\theta^\textsf{T}}\right]$

在 $\hat{\theta}_n$ 处的值 $I(\hat{\theta}_n)$ 来代替 $\hat{I}_n$。

定理. 设 $X_i\sim f(\cdot\mid\theta)$，先验分布为 $\pi(\theta)$。给定数据 $\pmb x$，当 $n\rightarrow\infty$ 时，

$\theta\mid\pmb x\approx N(\mathbb E(\theta\mid\pmb x),\text{Var}(\theta\mid\pmb x))$，假设 $\theta$ 的均值和方差存在；
$\theta\mid\pmb x\approx N(\tilde{\theta},i^{-1}(\tilde{\theta}))$，其中 $\tilde{\theta}$ 为后验众数，$i(\theta)$ 为观测信息量 $i(\theta)=-\dfrac{\text{d}^2\log\pi(\theta\mid\pmb x)}{\text{d}\theta^2}$；
$\theta\mid\pmb x\approx N(\hat{\theta},(i^{\star})^{-1}(\hat{\theta}))$，其中 $\hat{\theta}$ 为 $\theta$ 的MLE，$i^\star(\theta)=-\dfrac{\text{d}^2\log f(\pmb x\mid\theta)}{\text{d}\theta^2}$。

例如，对二项分布 $X\mid\theta\sim B(n,\theta)$，而 $\theta$ 取共轭先验 $Beta(\alpha,\beta)$，则 $\theta$ 的后验分布为

$\theta\mid x\sim Beta(\alpha+x,\beta+n-x).$

对较大的 $n$，使用上述三种方法实现逼近。

使用后验期望和后验方差，可以得到 $\theta\mid x\approx N\left(\dfrac{\alpha+x}{\alpha+\beta+n},\dfrac{(\alpha+x)(\beta+n-x)}{(\alpha+\beta+n)^2(\alpha+\beta+n+1)}\right).$
使用后验众数 $\tilde{\theta}=\dfrac{\alpha+x-1}{\alpha+\beta+n-2}$，而 $\dfrac{\text{d}^2\log\pi(\theta\mid x)}{\text{d}\theta^2}=-\dfrac{\alpha+x-1}{\theta^2}-\dfrac{\beta+n-x-1}{(1-\theta)^2},$
因此 $i(\tilde{\theta})=\dfrac{(\alpha+\beta+n-2)^3}{(\alpha+x-1)(\beta+n-x-1)}$，所以
$\theta\mid x\approx N\left(\dfrac{\alpha+x-1}{\alpha+\beta+n-2},\dfrac{(\alpha+x-1)(\beta+n-x-1)}{(\alpha+\beta+n-2)^3}\right).$
使用极大似然估计 $\hat{\theta}=\dfrac{x}{n}$，而 $i^\star(\hat{\theta})=\dfrac{n^3}{x(n-x)}$，所以 $\theta\mid x\approx N\left(\dfrac{x}{n},\dfrac{x(n-x)}{n^3}\right).$

alpha <- beta <- 2
n <- 50
x <- 20

# (1) posterior expectation and variation
n_mu1 <- (alpha + x) / (alpha + beta + n)
n_sigma1 <- n_mu1 * (beta + n - x) / (alpha + beta + n) / (alpha + beta + n + 1)

# (2) posterior MAP
n_mu2 <- (alpha + x - 1) / (alpha + beta + n - 2)
n_sigma2 <- n_mu2 * (beta + n - x - 1) / (alpha + beta + n - 2)^2

# (3) MLE
n_mu3 <- x / n
n_sigma3 <- x * (n - x) / n^3

rbind(c(n_mu1, n_sigma1), c(n_mu2, n_sigma2), c(n_mu3, n_sigma3))

          [,1]        [,2]
[1,] 0.4074074 0.004389575
[2,] 0.4038462 0.004629893
[3,] 0.4000000 0.004800000

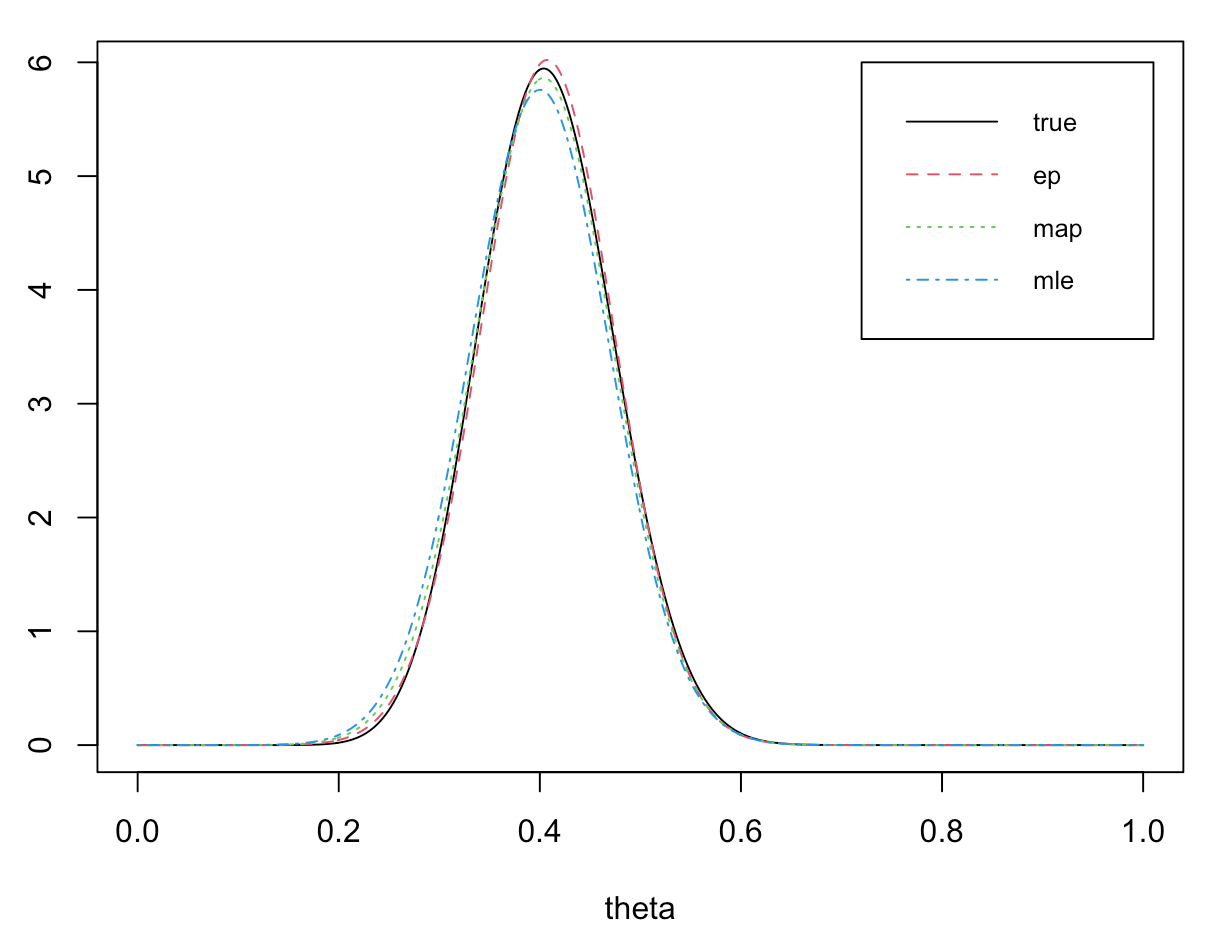
可以看到三种逼近的效果基本上类似，下面的密度函数图像也可以说明这一现象。

theta <- seq(0, 1, 0.001)
y1 <- dbeta(theta, alpha + x, beta + n - x)
y2 <- dnorm(theta, n_mu1, sqrt(n_sigma1))
y3 <- dnorm(theta, n_mu2, sqrt(n_sigma2))
y4 <- dnorm(theta, n_mu3, sqrt(n_sigma3))
plot(theta, y1, type = "l")
lines(theta, y2, col = 2, lty = 2)
lines(theta, y3, col = 3, lty = 3)
lines(theta, y4, col = 4, lty = 4)
legend(0.72, 6, legend = c('true', 'ep', 'map', 'mle'), col = 1:4, lty = 1:4,
       cex = 0.8, x.intersp = 0.8, y.intersp = 0.8)

在一些情况下，上述渐近正态性可能不成立，例如：

$\theta_t$ 位于参数空间 $\Theta$ 的边界上；
先验分布在 $\theta_t$ 处的质量为0；
后验分布是不正常的；
模型是不可识别的。

定理. 在一些正则条件下，

后验分布 $\sqrt{n}(\theta-\hat{\theta})\mid\pmb x$ 趋于正态分布 $N(0,I^{-1}(\theta_0))$；
后验分布 $\sqrt{n}(\theta^\star-\theta_0)\mid\pmb x$ 趋于正态分布 $N(0,I^{-1}(\theta_0))$，

其中 $\hat{\theta}$ 为极大似然估计，$\theta^\star$ 为后验期望，$\theta_0$ 为真值。

Laplace逼近

在Lec6.1贝叶斯计算方法中我们已经介绍了Laplace逼近的公式：

$\displaystyle I=\int_{-\infty}^{+\infty}\text{e}^{-nh(\theta)}\text{d}\theta\sim\text{e}^{-nh(\hat{\theta})}\dfrac{\sqrt{2\pi}}{\sqrt{nc}}\left[1+O(n^{-1})\right],$

其中 $c=h’’(\hat{\theta})$，$\hat{\theta}$ 为唯一的极大似然估计或后验众数（即要求 $h(\theta)$ 是单峰的）。

在贝叶斯近似计算中，后验特征

$\mathbb E^\pi[g(\theta)\mid\pmb x]=\dfrac{\int_{\mathbb R^k}g(\theta)f(\pmb x\mid\theta)\pi(\theta)\text{d}\theta}{\int_{\mathbb R^k}f(\pmb x\mid\theta)\pi(\theta)\text{d}\theta}$

可通过如下Laplace逼近近似计算：

对分子而言， $h^\star(\theta)=-\dfrac{\log g(\theta)+\log f(\pmb x\mid\theta)+\log\pi(\theta)}{n},\hat{\theta}=\underset{\theta\in\Theta}{\arg\max}~h^\star(\theta),\Sigma^\star=\dfrac{\partial^2h^\star(\theta)}{\partial\theta\partial\theta^\textsf{T}}\Big\vert_{\theta=\hat{\theta}},$
对分母而言， $h(\theta)=-\dfrac{\log f(\pmb x\mid\theta)+\log\pi(\theta)}{n},\tilde{\theta}=\underset{\theta\in\Theta}{\arg\max}~h(\theta),\Sigma=\dfrac{\partial^2h(\theta)}{\partial\theta\partial\theta^\textsf{T}}\Big\vert_{\theta=\tilde{\theta}},$

于是

$\mathbb E^\pi[g(\theta)\mid\pmb x]\approx\dfrac{g(\hat{\theta})f(\pmb x\mid\hat{\theta})\pi(\hat{\theta})\vert\Sigma^\star\vert^{-1/2}}{f(\pmb x\mid\tilde{\theta})\pi(\tilde{\theta})\vert\Sigma\vert^{-1/2}}.$

例如，对二项分布 $X\mid\theta\sim B(n,\theta)$，而 $\theta$ 取共轭先验 $Beta(\alpha,\beta)$，则 $\theta$ 的后验密度为

$\pi(\theta\mid x)\propto\theta^{\alpha+x-1}(1-\theta)^{\beta+n-x-1},\quad 0<\theta<1.$

因此这里

$h(\theta)=-\dfrac{(\alpha+x-1)\log\theta+(\beta+n-x-1)\log(1-\theta)}{n}\Rightarrow\tilde{\theta}=\dfrac{\alpha+x-1}{\alpha+\beta+n-2}.$

考虑后验均值 $\mathbb E^\pi(\theta\mid\pmb x)$ 的Laplace近似，则

$h^\star(\theta)=-\dfrac{(\alpha+x)\log\theta+(\beta+n-x-1)\log(1-\theta)}{n}\Rightarrow\hat{\theta}=\dfrac{\alpha+x}{\alpha+\beta+n-1}.$

而

$\Sigma=\dfrac{(\alpha+\beta+n-2)^3}{n(\alpha+x-1)(\beta+n-x-1)},\quad\Sigma^\star=\dfrac{(\alpha+\beta+n-1)^3}{n(\alpha+x)(\beta+n-x-1)},$

所以后验均值的Laplace近似为

$\dfrac{(\alpha+x)^{\alpha+x+1/2}}{(\alpha+x-1)^{\alpha+x-1/2}}\cdot\dfrac{(\alpha+\beta+n-2)^{\alpha+\beta+n-1/2}}{(\alpha+\beta+n-1)^{\alpha+\beta+n+1/2}}.$

对于 $\alpha=\beta=2$，$n=50$，$x=20$，近似结果为0.4073235。

贝叶斯变分推断

变分推断的基本思想是找一个与后验分布“近”的容易计算的分布，将推断问题转化为优化问题。

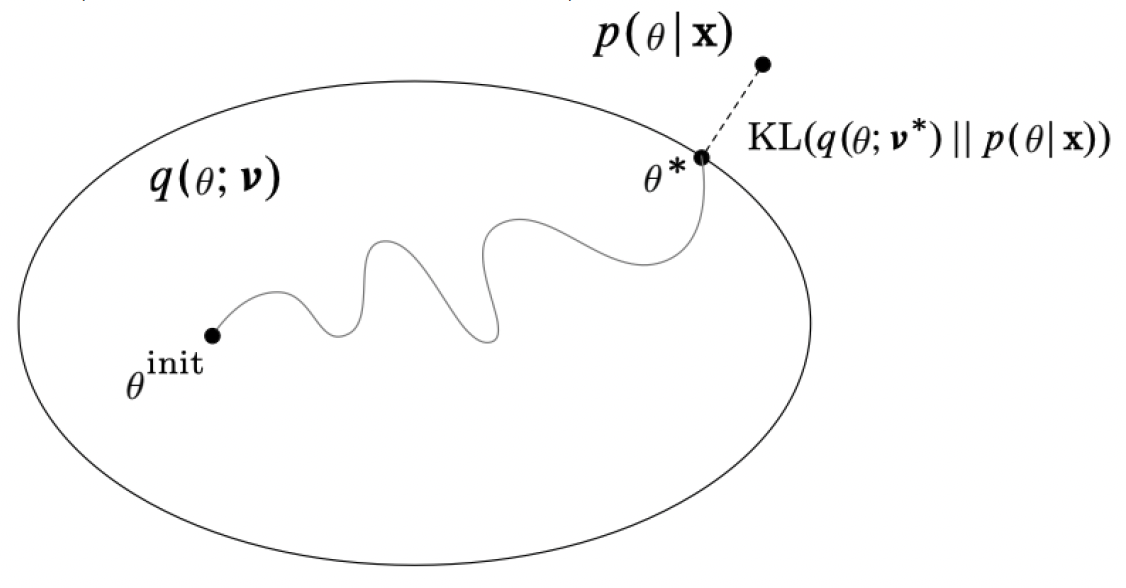
对隐变量 $\theta$，假设一个变分分布族 $q(\theta;\nu)$（容易计算），选择最优的变分参数 $\nu^\star$ 使得分布 $q^\star(\theta)=q(\theta;\nu^\star)$ 在KL距离（或其它准则）下最接近精确后验分布 $p(\theta\mid\pmb x)$。

注意到

$\begin{array}{rl} KL(q\|p)=&\!\!\!\!\displaystyle\int q(\theta)\log\dfrac{q(\theta)}{p(\theta\mid\pmb x)}\text{d}\theta\\ =&\!\!\!\!\displaystyle\int q(\theta)\log\dfrac{q(\theta)p(\pmb x)}{p(\pmb x\mid\theta)p(\theta)}\text{d}\theta\\ =&\!\!\!\!\displaystyle\log p(\pmb x)-\int q(\theta)\log\dfrac{p(\pmb x\mid\theta)p(\theta)}{q(\theta)}\text{d}\theta, \end{array}$

称第一部分为对数证据（evidence），第二部分为证据下界（ELBO）。于是

$q^\star=\underset{q\in Q}{\arg\min}~KL(q\|p)=\underset{q\in Q}{\arg\max}~ELBO(q).$

平均场变分推断

平均场变分推断（Mean-field variational inference，MFVI）就是考虑一类满足如下条件的分布族

$\displaystyle Q=\left\{q:q(\theta)=\prod_{j=1}^Jq_j(\theta_j)\right\}.$

即认为 $\theta=(\theta_1,\dots,\theta_J)$ 的各个分量是相互独立的。这就简化了ELBO的计算：

$\begin{array}{rl} ELBO(q)=&\!\!\!\!\displaystyle\int q(\theta)\log\dfrac{p(\pmb x\mid\theta)p(\theta)}{q(\theta)}\text{d}\theta\\ =&\!\!\!\!\displaystyle\int\left[\prod_{j=1}^Jq_j\right]\left[\log p(\pmb x,\theta)-\sum_{j=1}^J\log q_j\right]\text{d}\theta\\ \simeq&\!\!\!\!\displaystyle\int q_j\int\left[\prod_{i\neq j}q_i\right]\log p(\pmb x,\theta)\text{d}\theta_{i\neq j}\text{d}\theta_j-\int q_j\log q_j\text{d}\theta\\ \simeq&\!\!\!\!\displaystyle\int q_j\log\tilde{p}(\theta_j)\text{d}\theta_j-\int q_j\log q_j\text{d}\theta\\ =&\!\!\!\!-KL(q_j\|\tilde{p}), \end{array}$

这里 $\simeq$ 表示至多差一个可加常数，而 $\tilde{p}$ 满足

$\displaystyle\log\tilde{p}(\theta_j)\simeq\int\left[\prod_{i\neq j}q_i\right]\log p(\pmb x,\theta)\text{d}\theta_{i\neq j}=\mathbb E_{q_{i\neq j}}[\log p(\pmb x,\theta)].$

因此，使用坐标下降法，对 $j=1,\dots,J$ 有

$\begin{array}{rl} q_j^\star=&\!\!\!\!\underset{q\in Q}{\arg\max}~ELBO(q)=\underset{q\in Q}{\arg\min}~KL(q_j\|\tilde{p})=\tilde{p}(\theta_j)\\ \propto&\!\!\!\!\exp\left\{\mathbb E_{q_{i\neq j}}[\log p(\pmb x,\theta)\right\}]. \end{array}$

如果存在变分参数，即 $\displaystyle q(\theta)=\prod_{j=1}^Jq_j(\theta_j;\nu_j)$，并且

$\displaystyle p(\pmb x,\theta)=p(\pmb x)\prod_{j=1}^Jp(\theta_j\mid\theta_{1:(j-1)},\pmb x),$

那么

$\displaystyle ELBO(q)=\mathbb E_q\left[\log\dfrac{p(\pmb x,\theta)}{q(\theta;\nu)}\right]=p(\pmb x)+\sum_{j=1}^J\mathbb E_q\left[\log\dfrac{p(\theta_j\mid\theta_{1:(j-1)},\pmb x)}{q_j(\theta_j;\nu_j)}\right],$

从而对 $\nu_1,\dots,\nu_J$ 最大化等价于

$\nu_j^\star=\underset{\nu_j}{\arg\max}~\mathbb E_q\left[\log\dfrac{p(\theta_j\mid\theta_{1:(j-1)},\pmb x)}{q_j(\theta_j;\nu_j)}\right],\quad j=1,\dots,J.$

应用：主题模型

下面使用变分推断来解决一个更实际的例子——主题模型。主题模型是自然语言处理中最为关键的问题，用于分析大量文本的主题的分布。下面介绍隐狄利克雷分布（Latent Dirichlet Allocation）模型。

LDA模型是一种生成模型，它将文档视为一些主题的混合，其中主题共有 $K$ 个，语料库中的文档共有 $D$ 个，每篇文档中有 $N_d (d=1,\dots,D)$ 个词，而词典中一共包含 $V$ 个不同词。我们的目标是得到每篇文档的主题分布和每个主题中词的分布。模型的结构如下：

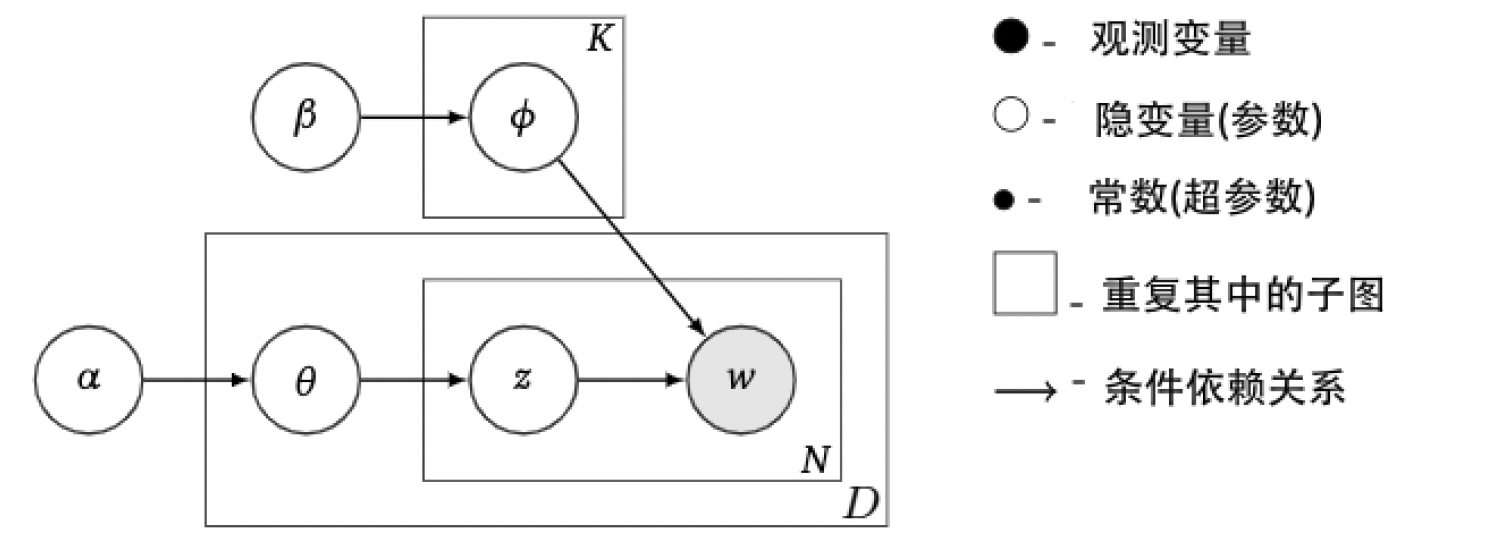
每个主题中词的分布来自Dirichlet分布 $\pmb\phi_k\sim\mathcal D(\pmb\beta)$，$k=1,\dots,K$，其中 $\pmb\beta$ 是 $V$ 维向量；
每篇文档中主题的分布来自Dirichlet分布 $\pmb\theta_d\sim\mathcal D(\pmb\alpha)$，$d=1,\dots,D$，其中 $\pmb\alpha$ 是 $K$ 维向量；
- 文档 $d$ 中第 $t$ 个主题来自 $\theta_d$ 的多项分布 $z_{d,t}\sim\mathcal{MB}(\pmb\theta_d)$，$t=1,\dots,N_d$；
- 文档 $d$ 中第 $t$ 个词来自对应主题 $\phi_{z_{d,t}}$ 的多项分布 $w_{d,t}\sim\mathcal{MB}(\pmb\phi_{z_{d,t}})$，$t=1,\dots,N_d$。

LDA假设文档之间相互独立，同一文档中的词相互独立，这样就有主题混合参数 $\Theta_{D\times K}$，主题标签 $\pmb z$，语料库中的词 $\pmb w$ 和主题 $\Phi_{K\times V}$ 的联合分布

$\begin{array}{rl} P(\pmb w,\pmb z,\Theta,\Phi\mid\pmb\alpha,\pmb\beta)=&\!\!\!\!\displaystyle\prod_{d=1}^Dp(\pmb w_d,\pmb z_d,\pmb\theta_d,\Phi\mid\pmb\alpha,\pmb\beta)\\ =&\!\!\!\!\displaystyle\prod_{d=1}^D\left\{P(\pmb\theta_d\mid\pmb\alpha)\prod_{t=1}^{N_d}P(z_{d,t}\mid\pmb\theta_d)P(w_{d,t}\mid\pmb\phi_{z_{d,t}})\times\prod_{i=1}^KP(\pmb\phi_k\mid\pmb\beta)\right\}. \end{array}$

我们感兴趣的是观测到词 $\pmb w$ 后的后验分布

$P(\pmb z,\Theta,\Phi\mid\pmb w,\pmb\alpha,\pmb\beta)=\dfrac{P(\pmb w,\pmb z,\Theta,\Phi\mid\pmb\alpha,\pmb\beta)}{P(\pmb w\mid\pmb\alpha,\pmb\beta)},$

其中

$\displaystyle P(\pmb w\mid\pmb\alpha,\pmb\beta)=\int_{\pmb\Phi}p(\Phi\mid\pmb\beta)\int_{\pmb\Theta}p(\Theta\mid\pmb\alpha)\sum_{\pmb Z}p(\pmb z\mid\Theta)p(\pmb w\mid\pmb z,\Phi)\text{d}\Theta\text{d}\Phi.$

这显然不能直接算出来，需要近似计算。Blei et al. (2003) 使用变分贝叶斯推断方法，考虑如下变分分布

$\begin{array}{rl} q(\Phi,\pmb z,\Theta\mid\pmb\lambda,\pmb\pi,\pmb\gamma)=&\!\!\!\!\displaystyle\prod_{d=1}^Dq(\pmb\theta_d,\pmb z_d,\Phi\mid\pmb\gamma_d,\pmb\pi_d,\pmb\lambda)\\ =&\!\!\!\!\displaystyle\prod_{d=1}^D\left\{q_d(\pmb\theta_d\mid\pmb\gamma_d)\prod_{t=1}^{N_d}q_d(z_{d,t}\mid\pi_{d,t})\prod_{i=1}^K\mathcal D(\pmb\phi_i\mid\pmb\lambda_i)\right\}, \end{array}$

其中 $\pmb\gamma_d,\pmb\pi_d=(\pi_{d,1},\dots,\pi_{d,N_d})$ 为文档 $d$ 的变分分布 $q_d(\cdot)$ 的参数。

（解法一：直接最大化ELBO）注意到

$\begin{array}{rl} ELBO(q)=&\!\!\!\!\displaystyle\mathbb E_q\left[\log\dfrac{p(\pmb w,\pmb z,\Theta,\Phi\mid\pmb\alpha,\pmb\beta)}{q(\pmb z,\Theta,\Phi\mid\pmb\lambda,\pmb\pi,\pmb\gamma)}\right]\\ =&\!\!\!\!\displaystyle\sum_{d=1}^D\mathbb E_q\left[\log\dfrac{p(\pmb w_d,\pmb z_d,\pmb\theta_d,\Phi\mid\pmb\alpha,\pmb\beta)}{q(\pmb\theta_d,\pmb z_d,\Phi\mid\pmb\gamma_d,\pmb\pi_d,\pmb\lambda)}\right]\\ =&\!\!\!\!\displaystyle\sum_{d=1}^D\left\{\mathbb E_d\left[\log\dfrac{p_d(\pmb w_d,\pmb z_d,\pmb\theta_d\mid\Phi,\pmb\alpha)}{q_d(\pmb\theta_d,\pmb z_d\mid\pmb\gamma_d,\pmb\pi_d)}\right]+\mathbb E_q\log\dfrac{p(\Phi\mid\pmb\beta)}{q(\Phi\mid\pmb\lambda)}\right\}, \end{array}$

这里 $\mathbb E_d$ 表示在 $q_d=q_d(\pmb\theta_d,\pmb z_d\mid\pmb\gamma_d,\pmb\pi_d)$ 分布下计算期望。因此，我们可以关注于第 $d$ 个文档，注意到

$\begin{array}{rl} \mathbb E_d\left[\log\dfrac{p_d(\pmb w_d,\pmb z_d,\pmb\theta_d\mid\Phi,\pmb\alpha)}{q_d(\pmb\theta_d,\pmb z_d\mid\pmb\gamma_d,\pmb\pi_d)}\right]=&\!\!\!\!\mathbb E_d\log p_d(\pmb w_d,\pmb z_d,\pmb\theta_d\mid\Phi,\pmb\alpha)-\log q_d(\pmb\theta_d,\pmb z_d\mid\pmb\gamma_d,\pmb\pi_d)\\ =&\!\!\!\!\mathbb E_d\big[\log p_d(\pmb\theta_d\mid\pmb\alpha)+\log p_d(\pmb z_d\mid\pmb\theta_d)+\log p_d(\pmb w_d\mid\pmb z_d,\Phi)\\ &-\log q_d(\pmb\theta_d\mid\pmb\gamma_d)-\log q_d(\pmb z\mid\pmb\pi)\big]\\ :=&\!\!\!\! l(\pmb\gamma_d,\pmb\pi_d\mid\Phi,\pmb\alpha). \end{array}$

下面分别计算各项。

首先 $\pmb\theta_d\mid\pmb\alpha\sim\mathcal D(\pmb\alpha)$，在 $q_d$ 分布下 $\pmb\theta\mid\pmb\gamma\sim\mathcal D(\pmb\gamma)$，因此第一项 $\begin{array}{rl} \mathbb E_d\log p_d(\pmb\theta_d\mid\pmb\alpha)=&\!\!\!\!\displaystyle\sum_{i=1}^K(\alpha_i-k)\mathbb E_d\log\theta_{d,i}+Const\\ =&\!\!\!\!\displaystyle\sum_{i=1}^K(\alpha_i-1)\left[\psi(\gamma_{d,i})-\psi\bigg(\sum_{l=1}^K\gamma_{d,l}\bigg)\right]+Const, \end{array}$
这里 $\psi(x)=\dfrac{\text{d}\log\Gamma(x)}{\text{d}x}=\dfrac{\Gamma’(x)}{\Gamma(x)}$。
其次 $\pmb z_d\mid\pmb\theta_d\sim\mathcal{MB}(\pmb\theta_d)$，在 $q_d$ 分布下 $\pmb\theta\mid\pmb\gamma\sim\mathcal D(\pmb\gamma)$，$\pmb z_d\mid\pmb\pi_d\sim\mathcal{MB}(\pmb\pi_d)$，因此第二项 $\begin{array}{rl} \mathbb E_d\log p_d(\pmb z_d\mid\pmb\theta_d)=&\!\!\!\!\displaystyle\mathbb E_d\left[\sum_{t=1}^{N_d}\sum_{i=1}^K\pmb 1(z_{d,t}=i)\log\theta_{d,i}\right]+Const\\ =&\!\!\!\!\displaystyle\sum_{t=1}^{N_d}\sum_{i=1}^K\mathbb E_d[\pmb 1(z_{d,t}=i)]\cdot\mathbb E_d\log\theta_{d,i}+Const\\ =&\!\!\!\!\displaystyle\sum_{t=1}^{N_d}\sum_{i=1}^K\pi_{d,t,i}\left[\psi(\gamma_{d,i})-\psi\bigg(\sum_{l=1}^K\gamma_{d,l}\bigg)\right]+Const, \end{array}$
再次 $\pmb w_d\mid\pmb z_d,\Phi\sim\mathcal{MB}(\pmb\phi_{\pmb z_d})$，在 $q_d$ 分布下 $\pmb z_d\mid\pmb\pi_d\sim\mathcal{MB}(\pmb\pi_d)$，因此第三项 $\begin{array}{rl} \mathbb E_d\log p_d(\pmb w_d\mid\pmb z_d,\Phi)=&\!\!\!\!\displaystyle\mathbb E_d\left[\sum_{t=1}^{N_d}\sum_{i=1}^K\sum_{r=1}^V\pmb 1(z_{d,t}=i)\pmb 1(w_{d,t}=r)\log\phi_{i,r}\right]+Const\\ =&\!\!\!\!\displaystyle\sum_{t=1}^{N_d}\sum_{i=1}^K\sum_{r=1}^V\mathbb E_d[\pmb 1(z_{d,t}=i)]\pmb 1(w_{d,t}=r)\log\phi_{i,r}+Const\\ =&\!\!\!\!\displaystyle\sum_{t=1}^{N_d}\sum_{i=1}^K\sum_{r=1}^V\pi_{d,t,i}\pmb 1(w_{d,t}=r)\log\phi_{i,r}+Const, \end{array}$
又次在 $q_d$ 分布下，$\pmb\theta_d\mid\pmb\gamma_d\sim\mathcal D(\pmb\gamma_d)$，因此第四项 $\begin{array}{rl} \mathbb E_d\log q_d(\pmb\theta_d\mid\pmb\gamma_d)=&\!\!\!\!\displaystyle\log\Gamma\left(\sum_{i=1}^K\gamma_{d,i}\right)-\sum_{i=1}^K\log\Gamma(\gamma_{d,i})\\ &\displaystyle+\sum_{i=1}^K(\gamma_{d,i}-1)\left[\psi(\gamma_{d,i})-\psi\bigg(\sum_{l=1}^K\gamma_{d,l}\bigg)\right]+Const, \end{array}$
最后在 $q_d$ 分布下 $\pmb z_d\mid\pmb\pi_d\sim\mathcal{MB}(\pmb\pi_d)$，因此第五项 $\begin{array}{rl} \mathbb E_d\log q_d(\pmb z_d\mid\pmb\pi_d)=&\!\!\!\!\displaystyle\mathbb E_d\left[\sum_{t=1}^{N_d}\sum_{i=1}^K\pmb 1(z_{d,t}=i)\log\pi_{d,t,i}\right]+Const\\ =&\!\!\!\!\displaystyle\sum_{t=1}^{N_d}\sum_{i=1}^K\mathbb E[\pmb 1(z_{d,t}=i)]\log\pi_{d,t,i}+Const\\ =&\!\!\!\!\displaystyle\sum_{t=1}^{N_d}\sum_{i=1}^K\pi_{d,t,i}\log\pi_{d,t,i}+Const. \end{array}$

因此，

$\begin{array}{rl} l(\pmb\gamma_d,\pmb\pi_d\mid\Phi,\pmb\alpha)=&\!\!\!\!\displaystyle\sum_{i=1}^K(\alpha_i-1)\left[\psi(\gamma_{d,i})-\psi\bigg(\sum_{l=1}^K\gamma_{d,l}\bigg)\right]\\ &\!\!\!\!\displaystyle+\sum_{t=1}^{N_d}\sum_{i=1}^K\pi_{d,t,i}\left[\psi(\gamma_{d,i})-\psi\bigg(\sum_{l=1}^K\gamma_{d,l}\bigg)\right]\\ &\!\!\!\!\displaystyle+\sum_{t=1}^{N_d}\sum_{i=1}^K\sum_{r=1}^V\pi_{d,t,i}\pmb 1(w_{d,t}=r)\log\phi_{i,r}-\log\Gamma\left(\sum_{i=1}^K\gamma_{d,i}\right)\\ &\!\!\!\!\displaystyle+\sum_{i=1}^K\log\Gamma(\gamma_{d,i})-\sum_{i=1}^K(\gamma_{d,i}-1)\left[\psi(\gamma_{d,i})-\psi\bigg(\sum_{l=1}^K\gamma_{d,l}\bigg)\right]\\ &\!\!\!\!\displaystyle-\sum_{t=1}^{N_d}\sum_{i=1}^K\pi_{d,t,i}\log\pi_{d,t,i}+Const. \end{array}$

注意到约束条件 $\displaystyle\sum\limits_{l=1}^K\pi_{d,t,l}=1$，因此使用Lagrange乘子法可得

$\displaystyle\pi_{d,t,i}\propto\phi_{i,w_{d,t}}\exp\left\{\psi(\gamma_{d,i})-\psi\bigg(\sum_{l=1}^K\gamma_{d,l}\bigg)\right\},$

其中 $\displaystyle\gamma_{d,i}=\alpha_i+\sum\limits_{t=1}^{N_d}\pi_{d,t,i}$。类似地，对于 $\Phi$ 分布中的参数，可以得到

$\displaystyle\lambda_{i,v}=\beta_v+\sum_{d=1}^D\sum_{t=1}^{N_d}\pi_{d,t,v}\pmb 1(w_{d,t}=v),$

而超参数 $\pmb\alpha$ 和 $\pmb\beta$ 可以通过变分EM算法估计（使用Newton法对 $\pmb\alpha$ 和 $\pmb\beta$ 求一阶、二阶导数，进而迭代求解）。

（解法二：利用坐标下降法）注意到

$\begin{array}{rl} \log p(\pmb w,\pmb z,\Theta,\Phi\mid\pmb\alpha,\pmb\beta)=&\!\!\!\!\displaystyle\sum_{d,t}\log p(w_{d,t}\mid z_{d,t},\Phi)+\sum_{d,t}\log p(z_{d,t}\mid\pmb\theta_d)\\ &\displaystyle+\sum_d\log p(\pmb\theta_d\mid\pmb\alpha)+\sum_k\log p(\pmb\phi_k\mid\pmb\beta)\\ =&\!\!\!\!\displaystyle\sum_{d,t}\sum_k\pmb 1(z_{d,t}=k)\log\phi_{k,w_{d,t}}+\sum_{d,t}\sum_k\pmb 1(z_{d,t}=k)\log\theta_{d,k}\\ &\displaystyle+\sum_{d,k}(\alpha_k-1)\log\theta_{d,k}+\sum_{k,v}(\beta_k-1)\log\phi_{k,v}+Const, \end{array}$

因此

对 $z_{d,t}$，有 $\begin{array}{rl} \log q^\star(z_{d,t})=&\!\!\!\!\mathbb E_{-z_{d,t}}[\log p(\pmb w,\pmb z,\Theta,\Phi\mid\pmb\alpha,\pmb\beta)]\\ =&\!\!\!\!\displaystyle\sum_k\pmb 1(z_{d,t}=k)\cdot\mathbb E_{q^\star}[\log\phi_{k,w_{d,t}}+\log\theta_{d,k}]+Const, \end{array}$
所以
$\pi_{d,t,k}=q^\star(z_{d,t}=k)\propto\exp\left(\mathbb E_{q^\star}[\log\phi_{k,w_{d,t}}+\log\theta_{d,k}]\right).$
对 $\pmb\theta_d$，有 $\begin{array}{rl} \log q^\star(\pmb\theta_d)=&\!\!\!\!\mathbb E_{-\pmb\theta_d}[\log p(\pmb w,\pmb z,\Theta,\Phi\mid\pmb\alpha,\pmb\beta)]\\ =&\!\!\!\!\displaystyle\sum_{k,t}\mathbb E_{q^\star}[\pmb 1(z_{d,t}=k)]\log\theta_{d,k}+\sum_k(\alpha_k-1)\log\theta_{d,k}+Const\\ =&\!\!\!\!\displaystyle\sum_{k,t}\pi_{d,t,k}\log\theta_{d,k}+\sum_k(\alpha_k-1)\log\theta_{d,k}+Const\\ =&\!\!\!\!\displaystyle\sum_k\left(\alpha_k-1+\sum_t\phi_{d,t,k}\right)\log\theta_{d,k}, \end{array}$
所以
$\displaystyle q^\star(\pmb\theta_d)=\mathcal D(\pmb\gamma_d),\quad\gamma_{d,k}=\alpha_k+\sum_t\pi_{d,t,k}.$
对 $\pmb\phi_k$，有 $\displaystyle q^\star(\pmb\phi_k)=\mathcal D(\pmb\lambda_k),\quad\lambda_{k,v}=\beta_v+\sum_{d,t}\pmb 1(w_{d,t}=v)\pi_{d,t,k}.$

后记

本文内容参考自中国科学技术大学《贝叶斯分析》（2022Fall）课件。

如对本文内容有任何疑问，请联系 watthu@mail.ustc.edu.cn。

Bayesian Approximate Inference