从本节起将逐步过渡到深度强化学习领域,首先介绍神经网络与深度学习的一些基本概念。
深度学习简介
传统机器学习
机器学习最核心的问题是在一系列可选函数映射中寻找一个最优的函数映射。因此
其中
- 表示(representation):确定假设空间(hypothesis space),即可选的函数映射类。
- 评价(evaluation):评价选出的函数的优劣,通常用损失函数来判定与实际的差距。
- 优化(optimization):需要一个搜索方法,能够在假设空间中找到评价函数得分最高的函数,即在训练集上有较低的损失。
PAC(Probably Approximately Correct)学习理论
记 $\cal X$ 为输入空间(input space),即样本或实例的所有可能取值的集合,$\cal Y$ 为标签或目标值的所有可能取值的集合。定义一个概念(concept)为 $c:\mathcal X\rightarrow\mathcal Y$ 是从 $\cal X$ 到 $\cal Y$ 的一个映射(规则),它属于一个概念类 $\cal C$。除此之外,我们假设所有的样本都是独立同分布的,满足一个固定的但是未知的分布 $\cal D$。
现在我们有一个学习器(learner),它由可能的概念构成,即假说集(hypothesis set),记作 $\cal H$,它不一定与 $\cal C$ 有重合。现在给予学习器样本 $S=(x_1,\dots,x_m)$ 与对应的标签 $(c(x_1),\dots,c(x_m))$(监督学习问题),其中每个样本都是根据分布 $\cal D$ 来独立同分布得到的,$c$ 是需要学习的目标概念,属于概念类 $\cal C$。
学习器需要根据带有标签的数据集 $S$,从假说集 $\cal H$ 中选择一个假说 $h_S$,该 $h_S$ 有着相对于目标概念 $c$ 很小的泛化误差(generalization error)。
- 泛化误差:给定 $h\in\cal H$,$c\in\cal C$,分布 $\cal D$,$h$ 的泛化误差(期望误差)为
$R(h)=\mathbb P_{x\sim\cal D}[h(x)\neq c(x)].$ - 经验误差:给定样本集合 $S=(x_1,\dots,x_m)$,则 $h$ 在 $S$ 上的经验误差(平均误差)为
$\displaystyle\hat{R}_S(h)=\dfrac{1}{m}\sum_{i=1}^m\pmb 1[h(x_i)\neq c(x_i)].$
一般来说,我们用经验误差来近似泛化误差,从而对学习器进行评估。
PAC学习理论考虑,能否从假设空间 $\cal H$ 中学习一个好的假设 $h$,它满足两个条件(PAC辨识条件):
- 近似正确(Approximately Correct):泛化误差 $R(h)$ 足够小,即存在一个足够小的 $\varepsilon>0$,使得
$R(h)\leq\varepsilon.$ - 可能正确(Probably Correct):$h$ 在很大概率上近似正确,即存在一个很小的 $\delta>0$,使得
$\mathbb P(R(h)\leq\varepsilon)\geq1-\delta.$
同时学习所需的样本数量不能太大,它是关于 $1/\varepsilon$、$1/\delta$、样本大小以及目标概念的规模的多项式函数。
定义. 一个概念类 $\cal C$ 称为PAC可学习,如果存在一个算法 $\cal A$ 和一个多项式函数 $\text{poly}(\cdot,\cdot,\cdot,\cdot)$ 满足对任意的 $\varepsilon>0$ 和 $\delta>0$,对所有 $\cal X$(具有 $n$ 个实例)上的分布 $\cal D$ 以及任意的目标策略 $c\in\cal C$,下式对满足 $m\geq\text{poly}(1/\varepsilon,1/\delta,n,\text{size}(c))$ 的任意样本量 $m$ 成立:
如果 $\cal A$ 跑得比 $\text{poly}(1/\varepsilon,1/\delta,n,\text{size}(c))$ 还快,那么 $\cal C$ 称为高效PAC可学习。如果这样的算法 $\cal A$ 存在,则它被称为针对 $\cal C$ 的PAC学习算法。
对目标概念 $c$ 在学习器的(有限)假设空间 $\mathcal H$ 中这种一致情形,有如下结论。
定理. 令 $\cal H$ 是从 $\cal X$ 到 $\cal Y$ 的映射的有限假设集合,算法 $\cal A$ 对任意概念 $c\in\cal H$ 和i.i.d.样本 $\cal S$ 的能够返回一个满足 $\hat{R}{\mathcal S}(h{\mathcal S})$ 的一致假设 $h_S$,则对任意的 $\varepsilon,\delta>0$,如果
就有不等式 $\mathbb P_{S\sim\mathcal D^m}[R(h_S)\leq\varepsilon]\geq1-\delta$ 成立。
因此,有限假设空间 $\cal H$ 都PAC可学习,所需的样本量如上所示,输出假设 $h$ 的泛化误差随样本量的增多而收敛到0,收敛速度为 $O(m^{-1})$。
对目标概念 $c$ 不在学习器的(有限)假设空间 $\mathcal H$ 中这种不一致情形(更通常),有如下结论。
定理. 设 $\cal H$ 为有限假设集合,$0<\delta<1$,则对任意 $h\in\cal H$,有
这就意味着,样本量 $m$ 较大时,$h$ 的经验误差可以作为其泛化误差的很好的近似。
深度学习
传统机器学习解决问题的思路是
其中中间三部分称为特征表达,它对最终算法的准确性起到非常关键的作用。
深度学习就是用来自动学习这些特征。深度学习主要有以下三步构成,下面一一进行介绍。
-
定义一系列函数(即神经网络)
神经网络中的一个重要概念是神经元,它接受来自其它神经元的信号,通过线性加权再进行激活得到最终的输出,即
$\displaystyle y=f(z)=f\left(\sum_{i=1}^nw_ix_i+b\right).$ 常用的激活函数如下表所示,具体的介绍将在深度学习部分展开。

神经网络设计的另一个关键是确定它的结构,在于网络的深度和每一层的宽度,其中深度主要取决于隐藏层的层数,而宽度取决于每一层的神经元的数量。
-
确定函数拟合效果(即损失函数)
首先我们需要准备训练数据,通过网络的学习可以得到模型的输出,而真实值与输出值之间的差距就是函数拟合效果的衡量,这就是损失函数,通常有均方损失和交叉熵损失。
-
选择最优函数(即优化)
我们希望的最优函数是能够最小化损失的函数,因此在有了一次损失函数值的结果后需要对参数进行更新,即优化,通常我们采用梯度下降方法。
前馈神经网络
最简单的前馈神经网络就是一个多层感知机,由一层输入层、多层隐藏层和一层输出层组成。
- 各神经元分别属于不同的层,层内无连接;
- 相邻两层之间的神经元全部两两连接;
- 整个网络无反馈,信号从输入层向输出层单向传播,可用一个有向无环图表示。
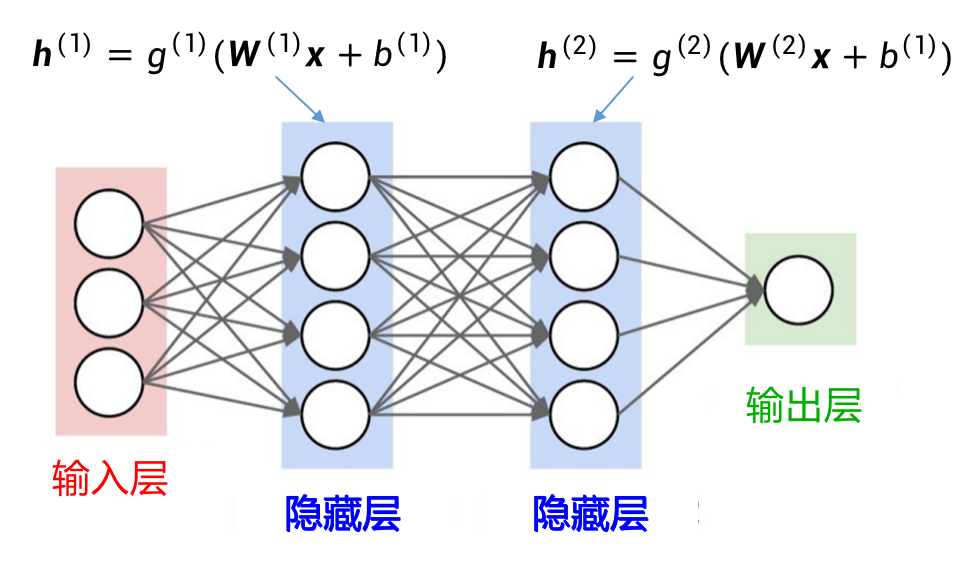
前馈神经网络通过下面的公式进行信息传播:
因此前馈神经网络可以通过逐层的信息传递,得到网络最后的输出 $\pmb a^{(L)}$:
给定一组样本 $(\pmb x^{(i)},y^{(i)}),~1\leq i\leq N$,用前馈神经网络的输出为 $f(\pmb x\mid\pmb W,\pmb b)$,则目标函数为
其中 $L(y^{(i)},\hat{y}^{(i)})$ 为损失函数,$|\pmb W|_F^2$ 为正则化项,用于防止过拟合。我们自然希望这个目标函数越小越好,因此梯度下降法的更新公式为
其中 $\alpha$ 是学习率。
这里进一步涉及到反向传播算法和批量学习(随机梯度下降),将在深度学习部分展开。
卷积神经网络(CNN)
如果用前馈神经网络来处理图像,会存在参数过多和局部不变性特征损失这两个问题,因此在卷积神经网络中,用卷积层代替全连接层来构建神经网络。
- 一维卷积:给定一个输入信号序列 $\pmb x$ 和滤波器 $f$,卷积的输出为
$\displaystyle y_t=\sum_{k=1}^mw_kx_{t-k+1}.$ - 二维卷积:给定图像的二维矩阵 $\pmb x$ 和滤波器 $f$,卷积的输出为
$\pmb y=\pmb w\otimes\pmb x$,即 $\displaystyle y_{ij}=\sum_{u=1}^m\sum_{v=1}^nw_{uv}\cdot x_{i-u+1,j-v+1}.$
可以看到,利用滤波器我们可以得到图像的局部视野信息。在实践中,滤波器涉及到滑动(stride)步长 $s$ 和零填充(paddle)$p$ 这两个重要参数,它和滤波器的大小共同决定了卷积输出结果的维度。
这样,通过卷积的输出我们得到的信息传播公式就改写为:
但是卷积层虽然减少了连接的个数,但是每一个特征映射的神经元个数并没有减少,解决这一问题的办法是池化(pooling):
- 最大池化(max pooling):取区域内所有神经元的最大值;
- 平均池化(average pooling):取区域内所有神经元的平均值。
于是,一般的卷积神经网络的结构是输入层、多个卷积块、全连接层交叉堆叠而成,其中卷积块又包含卷积、激活和池化等操作(有时还会引入Dropout操作用来防止过拟合)。
循环神经网络(RNN)
循环神经网络在时间序列数据中更加适用。给定一个输入序列 $\pmb x_{1:T}=(\pmb x_1,\pmb x_2,\dots,\pmb x_t,\dots,\pmb x_T)$,循环神经网络通过下面的公式更新带反馈边的隐藏层的活性值 $\pmb h_t$:
网络结构按时间展开如下图所示。
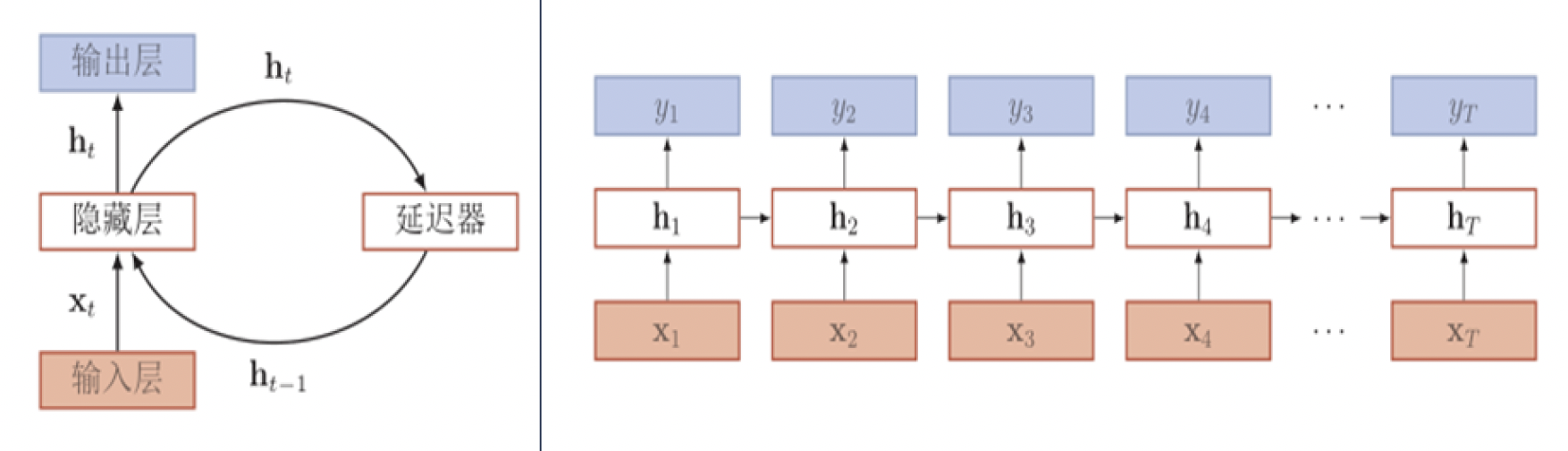
循环神经网络通过使用带自反馈的神经元,能够处理任意长度的序列,它比前馈神经网络更加符合生物神经网络的结构。
简单循环网络
最简单的循环网络是只有一个隐藏层的神经网络,隐藏层状态 $\pmb h_t$ 不仅与输入 $\pmb x_t$ 相关,也与上一时刻的隐藏层状态 $\pmb h_{t-1}$ 相关,其状态更新的公式为
设训练样本为输入序列 $\pmb x=(\pmb x_1,\dots,\pmb x_T)$ 和标签序列 $\pmb y=(\pmb y_1,\dots,\pmb y_T)$,则总损失函数为
梯度随着时间反向传播:可以计算梯度
其中 $\displaystyle\delta_{t,k}=\prod_{k=1}^{t-1}\left(\text{diag}(f’(\pmb z_k))\pmb U^\textsf{T}\right)\delta_{t,t}$,$\pmb z_k$ 为第 $k$ 步隐藏层神经元的净输入。
如果定义 $\gamma\simeq|\text{diag}(f’(\pmb z_i))\pmb U^\textsf{T}|$,则 $\delta_{t,k}=\gamma^{t-k}\delta_{t,t}$,因此
- 若 $\gamma>1$,则会造成系统不稳定,存在梯度爆炸问题;
- 若 $\gamma<1$,则会出现梯度消失的问题,
因此,我们只能学习到短周期的依赖关系,这就是所谓的长期依赖问题。
长短时记忆神经网络(LSTM)
为了解决长期依赖问题,LSTM中有选择性的遗忘,同时也有选择性的更新。在线性非线性依赖
的基础上,LSTM网络的改进主要在以下两个方面:
- 新的内部状态
- $\pmb c_t$ 专门进行线性的循环信息传递,同时(非线性)输出信息给隐藏层的外部状态 $\pmb h_t$;
- 在每个时刻 $t$,LSTM网络的内部状态 $\pmb c_t$ 记录了到当前时刻为止的历史信息;
- 门机制:控制信息传递的路径,取值在 $(0,1)$ 之间,表示以一定比例允许信息通过。
- 遗忘门 $\pmb f_t$ 控制上一个时刻的内部状态 $\pmb c_{t-1}$ 需要遗忘多少信息;
- 输入门 $\pmb i_t$ 控制当前时刻的候选状态 $\tilde{\pmb c}_t$ 有多少信息需要保存;
- 输出门 $\pmb o_t$ 控制当前时刻的内部状态 $\pmb c_t$ 有多少信息需要输出给外部状态 $\pmb h_t$。
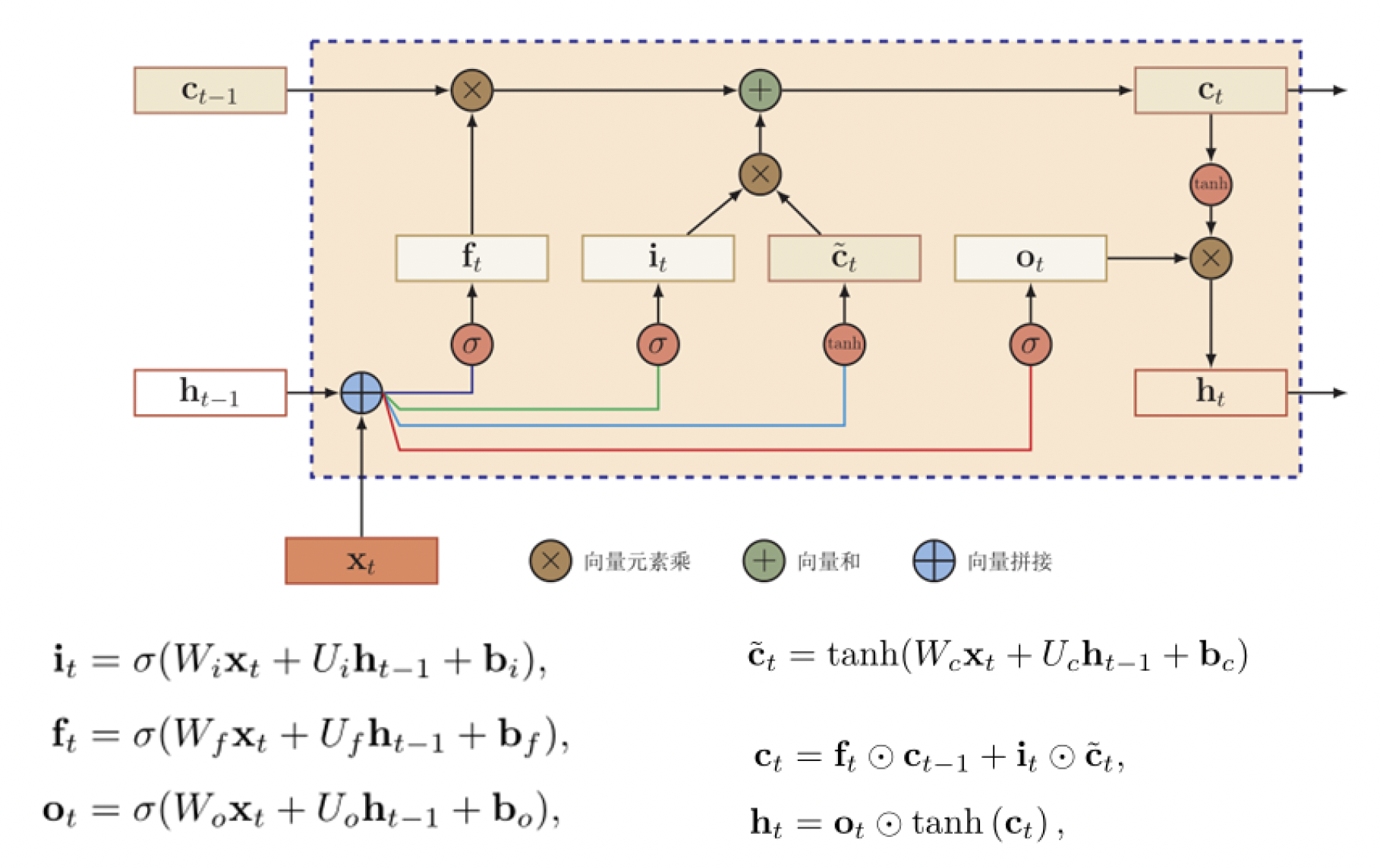
循环神经网络中的隐藏层状态 $\pmb h_t$ 存储了历史信息,可以看作是一种记忆(memory)。
- 在简单循环网络中,隐藏层状态每个时刻都会被重写,因此可以看作是一种短期记忆(short-term memory);
- 长期记忆(long-term memory)可以看作是网络参数,隐含了从训练数据中学到的经验,并更新周期要远远慢于短期记忆;
- 在LSTM网络中,记忆单元 $\pmb c_t$ 可以在某个时刻捕捉到某个关键信息,并有能力将此关键信息保存一定的时间间隔;
- 记忆单元 $\pmb c_t$ 中保存信息的生命周期要长于短期记忆 $\pmb h_t$,但又远远短于长期记忆,因此称为长的短期记忆(long short-term memory)。
后记
本文内容来自中国科学技术大学《强化学习》(2022Fall)课件。
如对本文内容有任何疑问,请联系 watthu@mail.ustc.edu.cn。