贝叶斯层次模型
层次模型并没有一个公认的定义,但是它的核心思想是“知道一个试验的一些信息就知道另外一个试验的一些信息”。对此,有四个关键观点:
- 对具有复杂结构的数据建模:例如学生嵌套在学校中、房屋嵌套在社区中等;
- 对异质性建模:例如房屋价格的波动性从一个社区到另一个社区;
- 对相依数据建模:结果随时间、空间、背景等变化而存在潜在复杂相依关系;
- 对背景因素建模:微观或宏观关系,例如单个房子价格依赖于其特点和社区的特点。
下面给出一些层次模型的例子:
- 医院手术死亡率
- 结构:病人嵌套在不同医院中。
- 问题:哪个医院的死亡率特别高或特别低?
- 环境暴露(THM)
- 结构:测量不同供水区域自来水中的三卤甲烷(THM)浓度。
- 问题:估计每个区域平均THM浓度以及THM浓度在各区域内和区域之间的波动性如何?
- 纵向临床试验
- 结构:每位病人重复观测。
- 问题:治疗效果上是否有差异?不同治疗方案下病人的响应是否有异质性?
- 教育成果
- 结构:英格兰学生16岁考试成绩,学生分为小学和中学(没有嵌套)。
- 问题:学生考试成绩中有多少波动性来自小学,多少来自中学?
- 单病例随机对照(N-of-1)试验
- 结构:对单个病人重复观测多种干预的差异。
- 问题:疗法是否有效?
上述例子都说明了一个基本建模问题:我们希望基于模型推断 $n$ 个“单元”(个体、地区、试验等)的各自参数 $\theta_1,\dots,\theta_n$,它们之间通过问题背景被联系起来。我们考虑下面三种不同的模型假设:
- 相同参数:所有 $\theta$ 都相同,此时数据可以混合起来,个体单元可以被忽略。
- 独立参数:所有 $\theta$ 是完全不相关的,此时每个单元的数据可以独立分析。
- 参数可交换:所有 $\theta$ 是相似的,即它们的标签没有信息,也就是说,假设 $\theta_1,\dots,\theta_n$ 来自同一个具有未知参数的先验分布。
例如,对英国自来水THM浓度问题,每年在70个供水区域里随机采样,关心每个区域的平均THM浓度。对每个区域的THM浓度假设正态似然
对残差的方差 $\sigma_{[e]}^2$,采用模糊先验 $\Gamma^{-1}(0.001,0.001)$,而对70个 $\theta_z$,有三种假设方式:
- 相同参数:所有 $\theta_z=\theta$,$z=1,\dots,70$,且指定正态先验 $N(\theta_0,\sigma_0^2)$,比如模糊先验
$\theta\sim N(0,100000).$ 在这一问题背景下,假设所有均值参数都相同显然是不合理的。
- 独立参数:所有 $\theta_z$ 相互独立,每个都指定一个正态先验,比如模糊先验
$\theta_z\sim N(0,100000),\quad z=1,\dots,70.$ 此时不同地区的数据之间独立,无法使用其他地区的数据。
- 参数可交换:假设 $\theta_1,\dots,\theta_{70}$ 来自同一个具有未知参数的先验分布,考虑如下的分层先验:
$\begin{array}{rl} \theta_z\sim&\!\!\!\! N(\mu,\sigma_{[z]}^2),\quad z=1,\dots,70,\\ \mu\sim&\!\!\!\! N(0,100000),\\ \sigma_{[z]}^2\sim&\!\!\!\!\Gamma^{-1}(0.001,0.001), \end{array}$ 其中 $\sigma_{[z]}^2$ 表示不同供水区域之间的THM浓度方差。
THM模型的图模型表示如下:
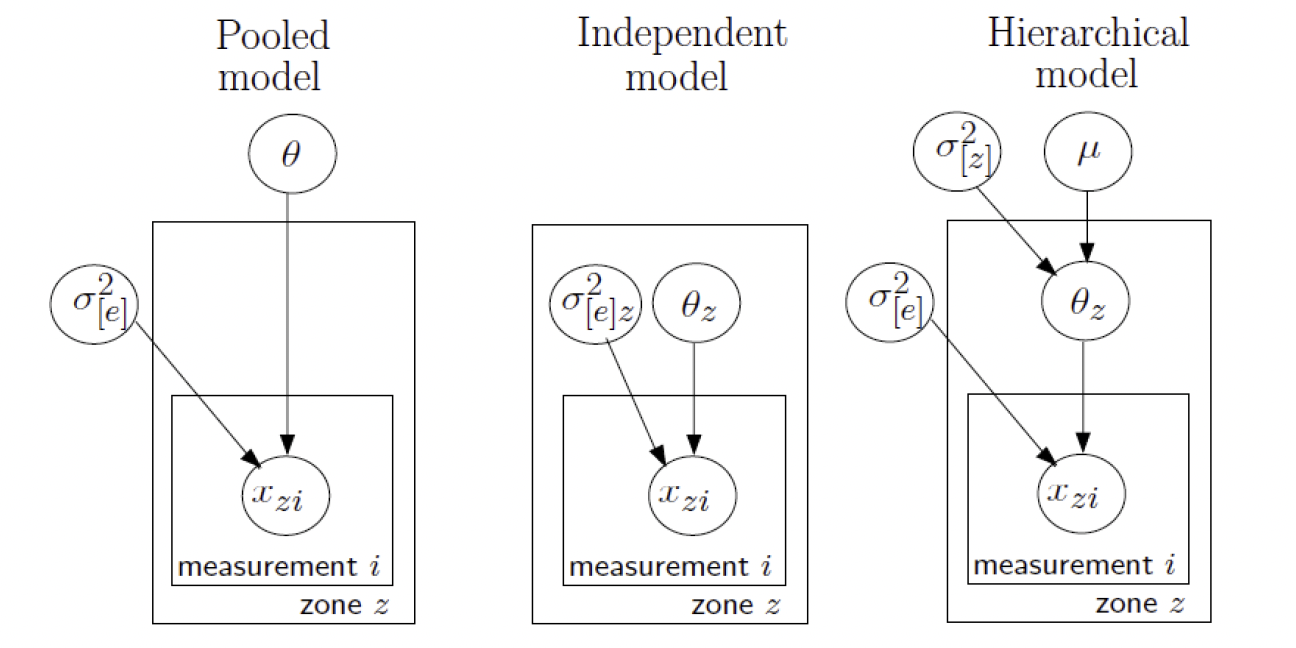
总的来说,层次模型看起来是我们观测到多组数据:
- 每个组有自己的参数 $X_{ij}\sim F_2(\mu_j)$;
- 参数的分布共享一些个超参数 $\mu_j\sim F_1(\theta)$;
- 这些超参数又有着自己的固定超参数 $\theta\sim F_0(\alpha)$。
实际数据生成过程是按照 $F_0,F_1,F_2$ 的顺序进行的。
下面我们来看其他组数据是如何影响当前组的参数推断的。考虑第 $i$ 组参数的后验分布为
记 $\pmb x_{-i}=(x_1,\dots,x_{i-1},x_{i+1},\dots,x_n)$,$\pmb\mu_{-i}=(\mu_1,\dots,\mu_{i-1},\mu_{i+1},\dots,\mu_n)$,上述被积函数第一项和第四项一起为 $p(\pmb x_{-i},\theta\mid\alpha)$,注意到
因此
这就说明了其他组数据通过超参数的分布影响了当前组的参数推断。
下面我们来看其他组数据是如何影响超参数 $\theta$ 的。注意到
视每个积分为 $p(\mu_j\mid\theta)$ 的加权平均:对每个 $\mu_j$,权重为 $p(\pmb x_j\mid\mu_j)$。假设每个积分被在一个点处的值所控制,记其为 $\hat{\mu}_j$,则可以视后验为
这就说明了其他组数据对超参数的影响是通过它们各自组的代表来进行的。
在层次模型中,响应变量的残差波动性被分为对应不同水平的不同部分,经常感兴趣的是高一层水平单元波动占总波动的百分比。例如,在简单2-水平正态线性模型中,我们可以用方差分解系数(VPC)
来衡量这一结果,其中 $\sigma_{[e]}^2$ 是第一层正态似然的方差,$\sigma_{[z]}^2$ 是第二层随机效应的方差。
下面看一个非正态的例子。考虑伦敦10年期间847个地区观测到的儿童白血病人数 $y_i$,$i=1,\dots,879$。使用全国年龄/性别标准化参考发病率,以及人口量,我们可以计算出每个地区期望的病例个数 $E_i$。使用贝叶斯层次模型进行分析如下。
对每个地区病例数假设Poisson似然
对879个 $\lambda_i$,有三种假设方式:
- 相同参数:所有 $\lambda_i=\lambda$,$i=1,\dots,879$,且指定伽马先验 $\Gamma(a,b)$,比如
$\lambda\sim\Gamma(1,1).$ - 独立参数:所有 $\lambda_i$ 相互独立,每个都指定一个伽马先验,比如
$\lambda_i\sim\Gamma(0.1,0.1),\quad i=1,\dots,879.$ 此时后验均值估计 $\hat{\lambda}_i\approx y_i/E_i$ 为极大似然估计(也称为标准化的发病率,SMR)。
- 参数可交换:假设 $\lambda_1,\dots,\lambda_{879}$ 来自同一个具有未知参数的先验分布,考虑如下的分层先验:
$\begin{array}{rl} \lambda_i\sim&\!\!\!\!\Gamma(a,b),\quad i=1,\dots,879,\\ a\sim&\!\!\!\! G_1,\quad b\sim G_2, \end{array}$ 自然的问题是什么样的超先验 $G_1,G_2$ 是合适的?这种做法不允许相邻地区的空间相依关系。
此时,$\log\lambda_i$ 正态随机效应模型似乎更加灵活,即对 $i=1,\dots,879$,考虑
其中超参数 $\sigma^2$ 和 $\alpha$ 可以取无信息先验,例如
此时我们感兴趣的参数为 $\lambda_i=\exp(\alpha+\theta_i)$,即第 $i$ 个地区相对于期望风险的相对风险和 $\sigma$,即对数相对风险在不同地区之间的标准偏差,这里的 $\theta_i$ 为随机效应,也可以被视为一个隐变量。
层次模型的先验
对于层次模型中的先验指定,需要区分
- 对主要感兴趣的参数,我们希望减少先验的影响;
- 对用于光滑的次要结构,一个(适度)有信息先验更合适。
在层次模型中,我们可能主要感兴趣第一层参数(回归系数等),或者方差分量(随机效应和它们的方差),或者两者都是。此外,先验最好施加在可解释参数上。
位置参数的先验
位置参数指均值、回归系数等,一般我们取在较大范围取值的均匀分布,或者方差很大的正态分布,例如
此时先验在似然支撑区域是局部均匀的。注意“宽”范围依赖于 $\theta$ 的尺度。
第一层参数的先验
对样本的方差 $\sigma^2$,通常采用标准Jeffreys先验
它等价于对数尺度下的均匀先验,而且从直观上是合理的,因为它完全忽略了参数的尺度(量级)。
超参数的先验
假设一个层次模型具有可交换的随机效应
常常希望对均值 $\mu$ 和随机效应方差 $\sigma^2$ 指定合理的无信息先验。
- 对位置参数,取值范围较大的均匀先验,或者具有大方差的正态先验,都可以使用。
- 对随机效应方差的无信息先验则比较有技巧性:
- Jeffreys无信息先验是不正常先验,作为第一层方差先验是可以使得后验正常,但是作为随机效应方差的先验,有可能导致后验不正常;
- $\Gamma(\varepsilon, \varepsilon)$,其中 $\varepsilon>0$ 非常小,是一个正常先验。$\Gamma(0.001,0.001)$ 常作为随机效应精度的先验,因为对正态分布具有很好的共轭性质,但是推断结果仍然可能对 $\varepsilon$ 的值敏感。
- 对标准偏差指定一个有限区间上的均匀分布 $\sigma\sim U(0,1000)$,上限的选择依赖于参数的尺度。
- 对标准差赋予半正态或半 $t$ 分布 $\sigma\sim N(0,100)\cdot I(0,)$。
纵向数据中的层次模型
所谓纵向数据是个体被依时间顺序重复观测所得到的数据,同一个体的观测之间是相关的。纵向数据有不同的形式,如连续或离散的响应变量、等间距或不等间距观测、每个个体观测时间点相同或不同、有或没有缺失数据、许多或很少时间点、许多或很少个体。
考虑抗抑郁症试验的例子,367个个体被随机分成3组,用以比较3种抑郁症疗法的效果。
- 每个个体每周来访一次,共5次(第0周是参加临床试验前,第1-4周是治疗期间);
- 使用Hamilton depression score(HAMD)评分对每个个体治疗效果进行评分;
- HAMD得分为0-50分,分值越高抑郁症越严重。
有些个体从第2周起退出试验(dropout),我们忽略掉这些退出的个体,分析其他246位完成试验的个体数据。数据如下图所示:
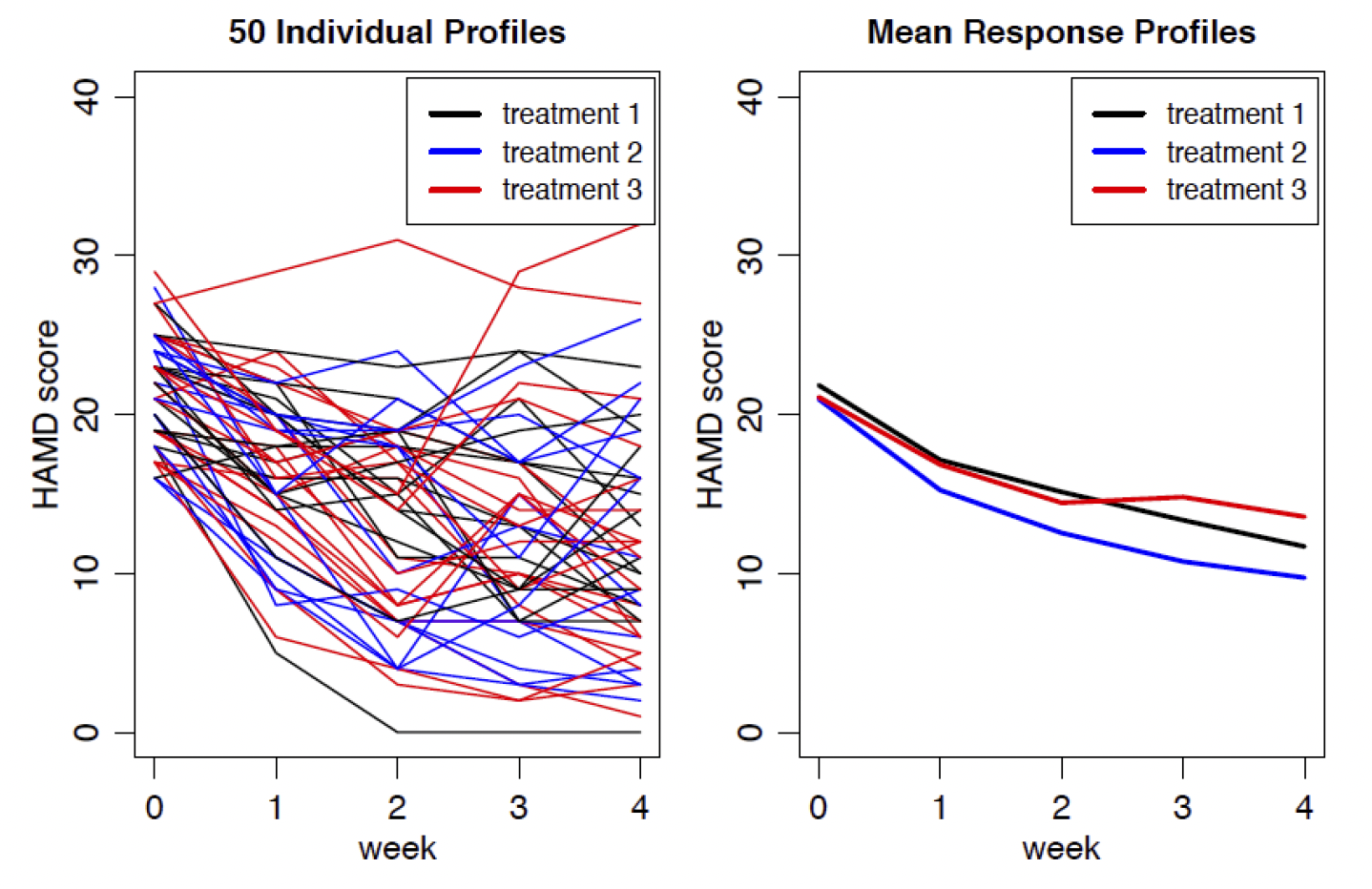
关心的问题是三种治疗方式得到的HAMD得分随时间变化有差异吗?记 $y$ 表示HAMD得分,$t$($t=1,2,3$) 表示处理,$w$($w=0,1,2,3,4$)表示星期,考虑三种模型:
- 标准线性模型(非层次模型)
先验分布取为
此模型下重复观测结构被忽略了。
- 随机效应模型(层次模型)
参数的先验分布取为
假设给定 $\alpha_i$ 时,${y_{iw},w=0,1,2,3,4}$ 相互独立,且 $\alpha_i\sim N(\mu_\alpha,\sigma_\alpha^2)$ 满足可交换性,$i=1,\dots,246$,超参数的先验分布取为
图模型表示如下:
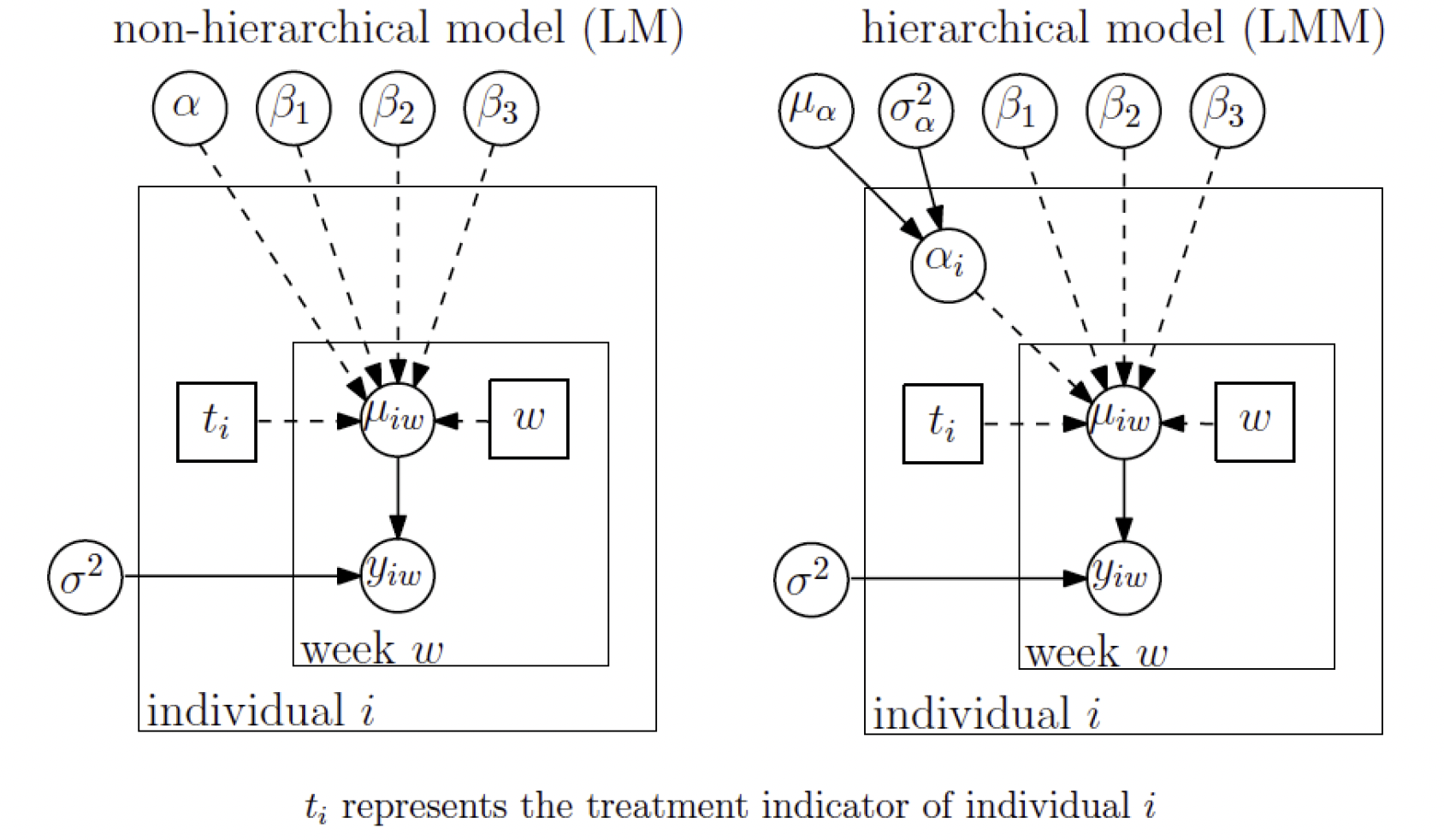
下图给出了两个模型下的拟合结果。
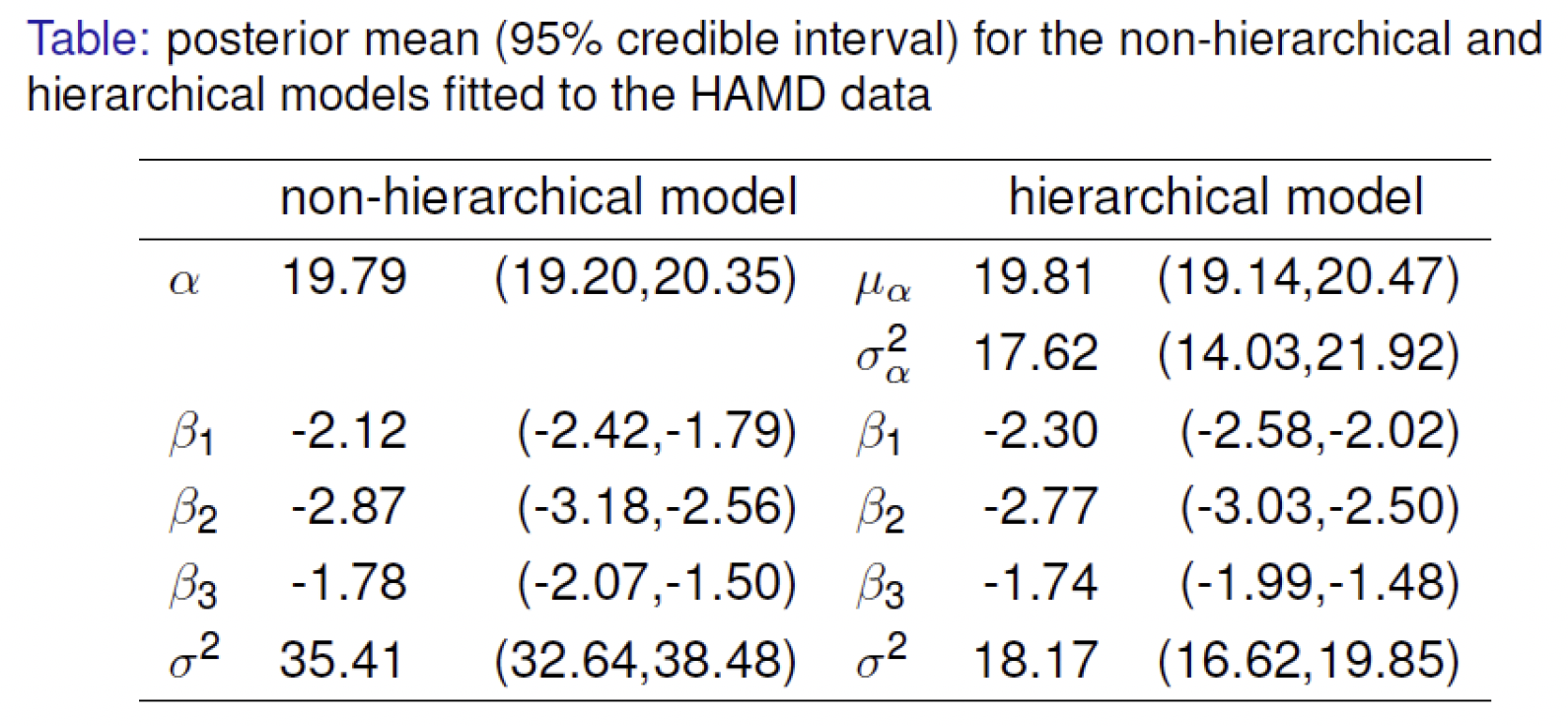
注意到残差方差 $\sigma^2$ 在引入了随机效应后有了明显的降低,另外,考虑层次模型中需要加入随机斜率,进一步对模型进行改进。假设
假设给定 $\alpha_i,\beta_{t_i,i}$ 时,${y_{iw},w=0,1,2,3,4}$ 相互独立,且 $\alpha_i\sim N(\mu_\alpha,\sigma_\alpha^2)$ 满足可交换性,$\beta_{1,i},\beta_{2,i},\beta_{3,i}$ 服从相同分布,$i=1,\dots,246$,超参数的先验分布取为
残差方差 $\sigma^2$ 的先验分布取为 $\sigma^2\sim\Gamma^{-1}(0.001,0.001)$。下图给出了最终的模型拟合结果。

- 自回归模型(AR1)
其中
而 $\varepsilon_{iw}\sim N(0,\sigma^2)$,$w=0,1,2,3,4$。下图是三种模型的拟合结果。
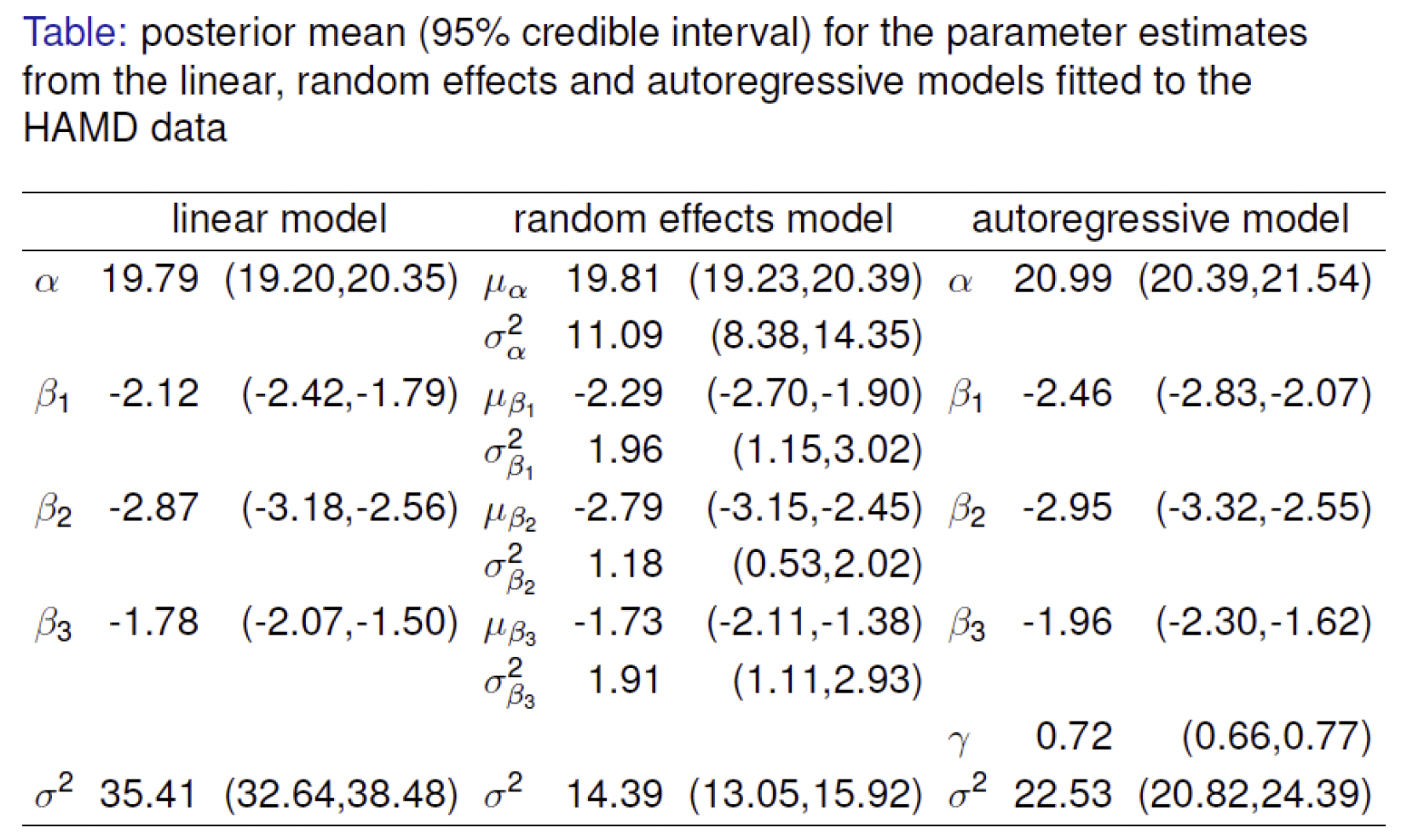
注意到不同处理下HAMD得分随时间变化差异体现在 $\beta_1-\beta_2$、$\beta_1-\beta_3$ 和 $\beta_2-\beta_3$ 或者在随机斜率模型中的 $\mu_{\beta_1}-\mu_{\beta_2}$、$\mu_{\beta_1}-\mu_{\beta_3}$ 和 $\mu_{\beta_2}-\mu_{\beta_3}$ 中。结果如下图所示。

缺失数据
贝叶斯层次模型很容易处理包含部分观测数据,集成关于缺失原因的假设模型。
前面的HAMD例子我们忽略了那些退出的个体,现在我们考虑对这些缺失模式进行建模。数据如下图所示:
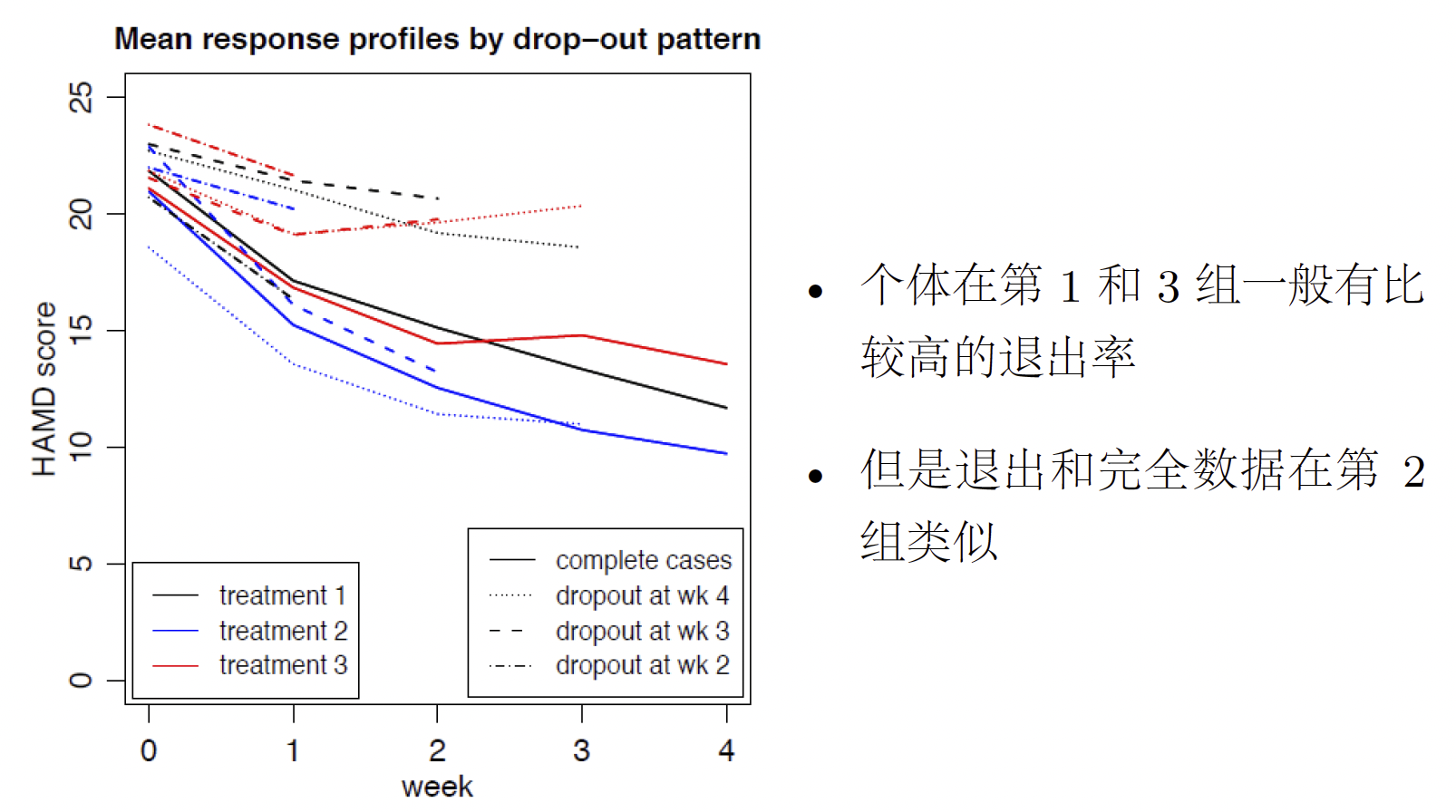
在原来模型的基础上,构建缺失指标
并且可以假设缺失的概率,即 $m_{iw}\sim\text{Bernoulli}(p_{iw})$。
- 完全随机缺失(MCAR):缺失不依赖于观测或未观测数据,如
$\text{logit}(p_{iw})=\theta_0.$ - 随机缺失(MAR):缺失依赖于观测数据,如
$\text{logit}(p_{iw})=\theta_0+\theta_1t_i,$ 或 $\text{logit}(p_{iw})=\theta_0+\theta_2y_{i0}.$ - 非随机缺失(MNAR):上述两种缺失模式均不成立,如
$\text{logit}(p_{iw})=\theta_0+\theta_3y_{iw}.$
缺失数据的联合建模
令 $\pmb z=(z_{ij}){n\times k}$ 表示数据阵,将 $\pmb z$ 划分为观测部分 $\pmb z^{\text{obs}}$ 和缺失部分 $\pmb z^{\text{mis}}$,令 $\pmb m=(m{ij})_{n\times k}$ 表示缺失指标
假设模型的未知参数为 $\beta$ 和 $\theta$,则完全数据下的联合模型为
观测数据下的似然函数为
注意到联合似然可以分解为
进一步如果有条件独立性,则
这种分解方法称为选择模型。于是观测数据下的似然函数
- 随机缺失(MAR)机制下,$f(\pmb m\mid\pmb z^{\text{obs}},\pmb z^{\text{mis}},\theta)=f(\pmb m\mid\pmb z^{\text{obs}},\theta)$,此时
$\begin{array}{rl} f(\pmb z^{\text{obs}},\pmb m\mid\beta,\theta)=&\!\!\!\!\displaystyle f(\pmb m\mid\pmb z^{\text{obs}},\theta)\int_{\pmb Z^{\text{mis}}}f(\pmb z^{\text{obs}},\pmb z^{\text{mis}}\mid\beta)\text{d}\pmb z^{\text{mis}}\\ =&\!\!\!\!f(\pmb m\mid\pmb z^{\text{obs}},\theta)f(\pmb z^{\text{obs}}\mid\beta). \end{array}$ - 完全随机缺失(MCAR)机制下,$f(\pmb m\mid\pmb z^{\text{obs}},\pmb z^{\text{mis}},\theta)=f(\pmb m\mid\theta)$,此时
$\begin{array}{rl} f(\pmb z^{\text{obs}},\pmb m\mid\beta,\theta)=&\!\!\!\!\displaystyle f(\pmb m\mid\theta)\int_{\pmb Z^{\text{mis}}}f(\pmb z^{\text{obs}},\pmb z^{\text{mis}}\mid\beta)\text{d}\pmb z^{\text{mis}}\\ =&\!\!\!\!f(\pmb m\mid\theta)f(\pmb z^{\text{obs}}\mid\beta). \end{array}$
如果缺失数据是MCAR或MAR,我们称缺失数据机制称为可忽略的。这里的“可忽略”表示我们可以忽略缺失机制模型,但不表示我们可以忽略缺失数据。如果数据机制是不可忽略的,那么就不能忽略缺失机制模型。
在HAMD例子中,下图给出了MCAR机制对处理比较的影响。

从图中可以看到使用所有数据提供了更强的证据:处理2比处理1更有效;处理2比处理3更有效。
对于MNAR机制,我们假设退出机制的模型为
其中 $\overline{y}$ 为平均值,$\theta_0,\theta_1$ 取无信息先验,得到如下图所示的比较结果。

最后需要做灵敏度分析,因为我们并不知道真实的缺失机制是什么。前面我们通过假设缺失是可忽略的,以及有信息的缺失机制来评估了结果,但是,我们还需要检查其他的有信息缺失机制,例如
- 允许退出概率依赖于得分的变化,即
$\text{logit}(p_{iw})=\theta_0+\theta_2(y_{i(w-1)}-\overline{y})+\theta_3(y_{iw}-y_{i(w-1)}).$ - 允许 $\theta$ 对不同处理有差异。
- 使用不同的先验分布。
灵敏度分析的比较结果如下图。
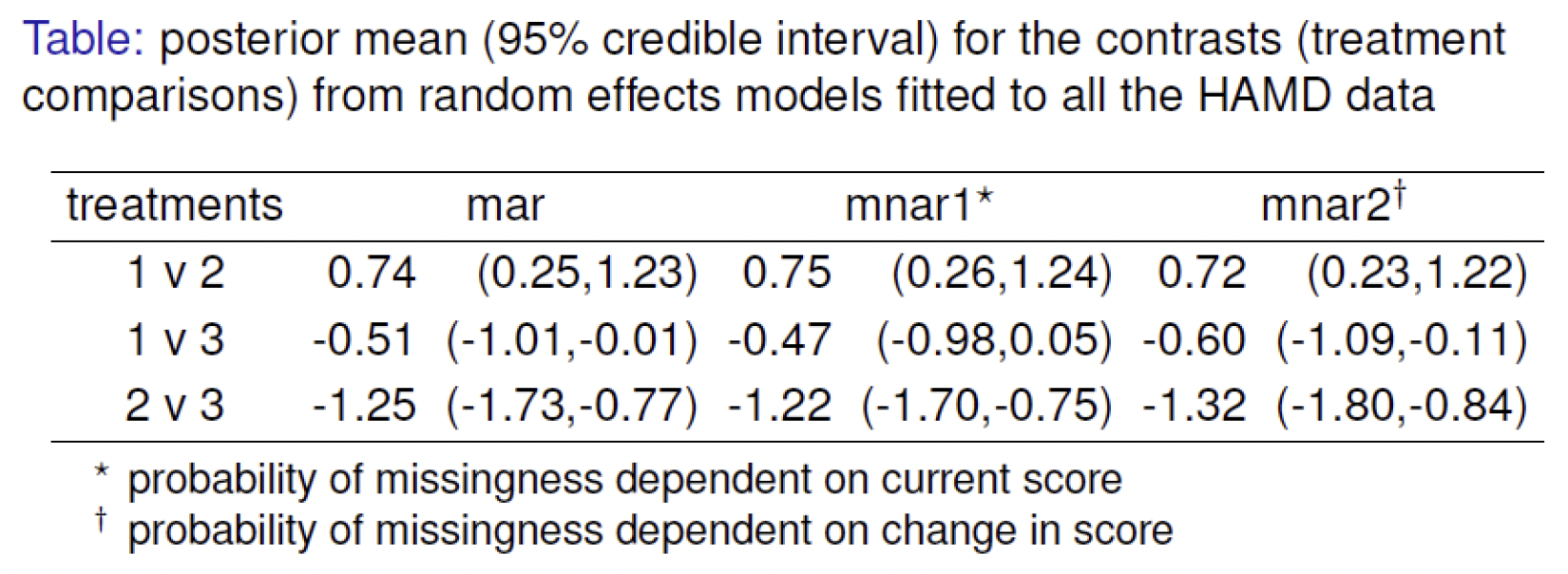
后记
本文内容参考自中国科学技术大学《贝叶斯分析》(2022Fall)课件。
如对本文内容有任何疑问,请联系 watthu@mail.ustc.edu.cn。