Q-Learning
回顾Q-Learning算法的更新公式为
而在行动值函数估计中,我们将Q函数进行参数化 $\hat{q}(s,a,\pmb w)\approx q_\pi(s,a)$,采用随机梯度下降寻找最接近真实Q函数的参数化表示,即
由此得到带参数的Q函数的梯度更新公式:
Q-Learning算法总结如下:
- 在环境中采取行动 $a_t$,得到 $(s_t,a_t,s_{t+1},r_{t+1})$;
- 计算目标 $\text{target}(s_t)=r_{t+1}+\gamma\max\limits_{a’\in\mathcal A}q(s_{t+1},a’,\pmb w)$;
- 更新参数 $\pmb w\leftarrow\pmb w+\alpha\big(\text{target}(s_t)-q(s_t,a_t,\pmb w)\big)\dfrac{\text{d}q(s_t,a_t,\pmb w)}{\text{d}\pmb w}$;
- 回到第一步。
这是拟合Q迭代(Fitted Q Iteration)的Online版本,因为Q-Learning在获得新的状态后立即更新参数,而拟合Q迭代则在完整经历下再更新参数,具体算法如下:
- 根据策略产生数据集 ${(s_t,a_t,s_{t+1},r_{t+1})}$;
- 迭代 $K$ 次:
- 计算目标 $\text{target}(s_t)=r_{t+1}+\gamma\max\limits_{a’\in\mathcal A}q(s_{t+1},a’,\pmb w)$;
- 更新参数 $\displaystyle\pmb w\leftarrow\underset{\pmb w}{\arg\min}\sum\limits_t\big|\text{target}(s_t)-q(s_t,a_t,\pmb w)\big|^2$。
下面给出了Q-Learning存在的一些问题。
-
问题1: Q-Learning并不是严格梯度下降的
注意到在计算梯度时,没有考虑目标对参数的梯度,而仅仅考虑 $q(s_t,a_t,\pmb w)$ 对 $\pmb w$ 的梯度,所以并不能保证参数收敛到全局最优解。
-
问题2: 只有一个样本
注意到在拟合Q迭代中,我们是首先产生了数据集进而进行参数更新。针对神经网络而言,Q-Learning这种仅提供一个样本来更新参数,往往会产生一些问题。
-
问题3: 目标的不断变化
在Q-Learning中,每次都重新根据新的参数计算了目标,然后再更新参数,会使得迭代产生困难。
-
问题4: 样本的相关性
产生的连续状态序列往往是高度相关的,可能会导致对当前环境状态的过拟合。
解决这些问题存在几种方案。
-
Replay Buffers
我们可以存储关于转移的数据集,从中采样一些转移进而使用梯度下降法更新参数。
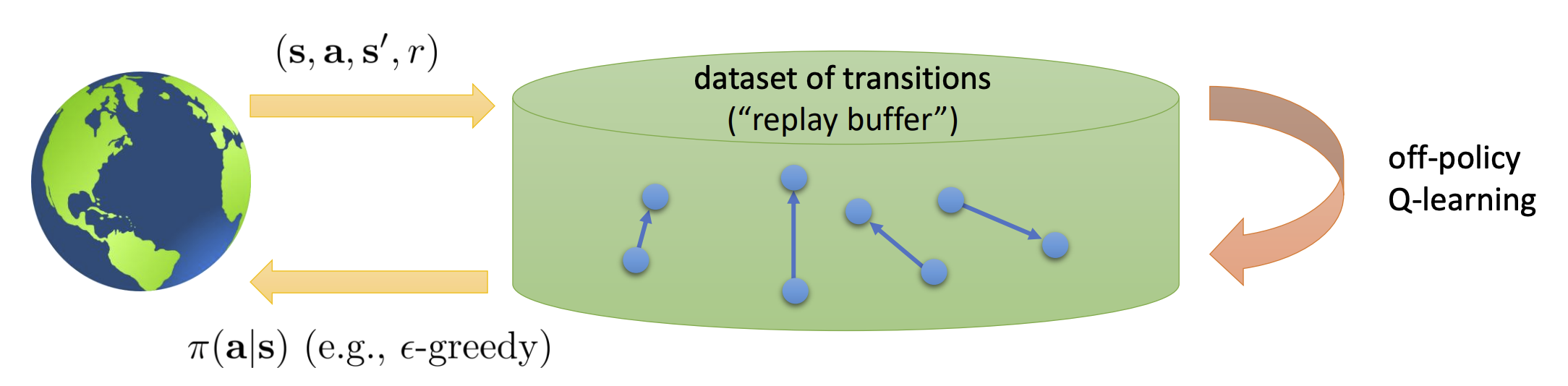
这一方案解决了只有一个样本和样本相关性的问题。
-
Target Networks
为了解决目标的不断变化问题,我们可以根据最近一次的参数 $\pmb w’$ 来得到固定版本的目标,而后再去更新新的参数 $\pmb w$,这就可以使得内部循环时目标是不变的。
带有Replay Buffer和Target Network的Q-Learning算法如下:
- 存储目标网络参数 $\pmb w’\leftarrow\pmb w$;
- 迭代 $N$ 次:
- 根据策略产生数据集 ${(s_t,a_t,s_{t+1},r_{t+1})}$,并添加到 $\cal B$ 中;
- 迭代 $K$ 次;
- 从 $\cal B$ 中采样一批 $(s_t,a_t,s_{t+1},r_{t+1})$;
- 更新参数 $\displaystyle\pmb w\leftarrow\pmb w+\alpha\sum\limits_t\big(r_{t+1}+\gamma\max\limits_{a’\in\cal A}q(s_{t+1},a’,\pmb w’)-q(s_t,a_t,\pmb w)\big)\dfrac{\text{d}q(s_t,a_t,\pmb w)}{\text{d}\pmb w}$。
Deep Q-Learning
根据带有Replay Buffer和Target Network的Q-Learning算法,我们就有了经典的DQN算法:
- 采取行动 $a_t$,得到 $(s_t,a_t,s_{t+1},r_{t+1})$,并将其加入 $\cal B$ 中;
- 从 $\cal B$ 中均匀地采样一批 $(s_t,a_t,s_{t+1},r_{t+1})$;
- 利用目标网络计算目标 $\text{target}(s_t)=r_{t+1}+\gamma\max\limits_{a’\in\cal A}q(s_{t+1},a’,\pmb w’)$;
- 更新参数 $\displaystyle\pmb w\leftarrow\pmb w+\alpha\sum\limits_t\big(\text{target}(s_t)-q(s_t,a_t,\pmb w)\big)\dfrac{\text{d}q(s_t,a_t,\pmb w)}{\text{d}\pmb w}$;
- 每 $N$ 步后更新 $\pmb w’\leftarrow\pmb w$;
- 回到第一步。
第五步中,有时也在每一步采用 $\pmb w’\leftarrow\tau\pmb w’+(1-\tau)\pmb w$(称为Polyak平均),常取 $\tau=0.999$。
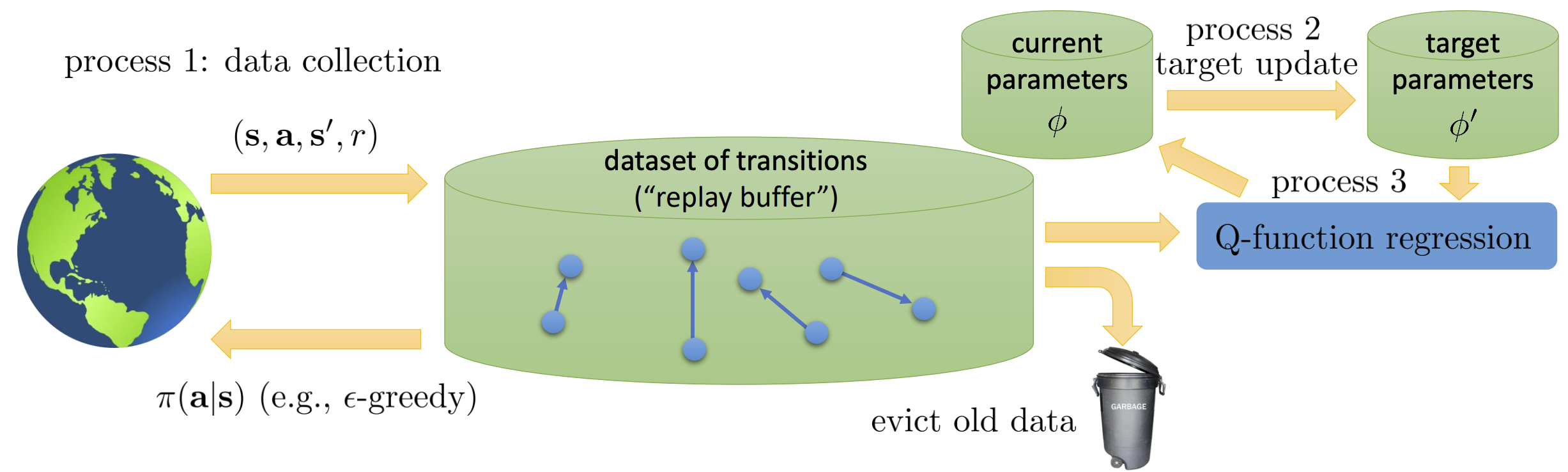
DQN的细节改进:
-
损失函数可以不用平方损失,而采用Huber损失:
$L_\delta(y,f(x))=\left\{\begin{array}{ll} \dfrac{1}{2}[y-f(x)]^2, & \vert y-f(x)\vert\leq\delta,\\ \delta\vert y-f(x)\vert+\dfrac{1}{2}\delta^2, & \vert y-f(x)\vert<\delta. \end{array}\right.$ - 随机梯度下降可以换成RMSprop等应用于神经网络参数更新的算法。
- $\varepsilon$-贪婪算法中的 $\varepsilon$ 可以逐步减少:一开始设置为1,而后慢慢减少到0.1或0.05等等。
DQN的一些改进
Double DQN
与Double Q-Learning类似的,为了避免最大化偏差的问题,我们用
- 当前网络 $\pmb w$ 来选择行动;
- 目标网络 $\pmb w’$ 来评估行动。
原来我们使用了双倍的内存,但是这里有一个天然的目标网络,所以并没有多余的内存消耗。具体来说,从公式角度,仅改变了目标的计算:
这里里面的 $\pmb w$ 原来采用的是 $\pmb w’$。

Prioritized Replay
简单来说,就是采用优先经验,对经验进行加权,在Buffer中采样时选择优先级高的经验。而经验的好坏可以用可改进量来衡量,即
通过优先采样学习,可以加快学习的速度。

注意到这里 $P(i)=\dfrac{p_i^\alpha}{\sum_kp_k^\alpha}$ 衡量了优先级,而 $\alpha$ 决定了优先度的把握,当 $\alpha=0$ 时退化为均匀采样的情形;$\tilde{w}_i=(NP(i))^{-\beta}$ 是重要性采样的权重,$\beta$ 会随着不断的训练从0增长到1。
在工程中,由于每次抽样都要根据优先级所有样本进行排序,这个代价很大,所以往往采用SumTree方法减少计算。
SumTree是一种树形结构,每个叶结点存储每个样本的优先级 $p$,每个非叶结点只有两个分叉,结点的值是两个分叉的和,所以根结点的值就是所有优先级的和。在实际采样时,首先根据要抽取的样本数将根结点的值进行区间划分,而后在每个区间内随机选取一个值,再进行自顶向下的路径选择,如图所示,给出了选取24的路径选择结果。
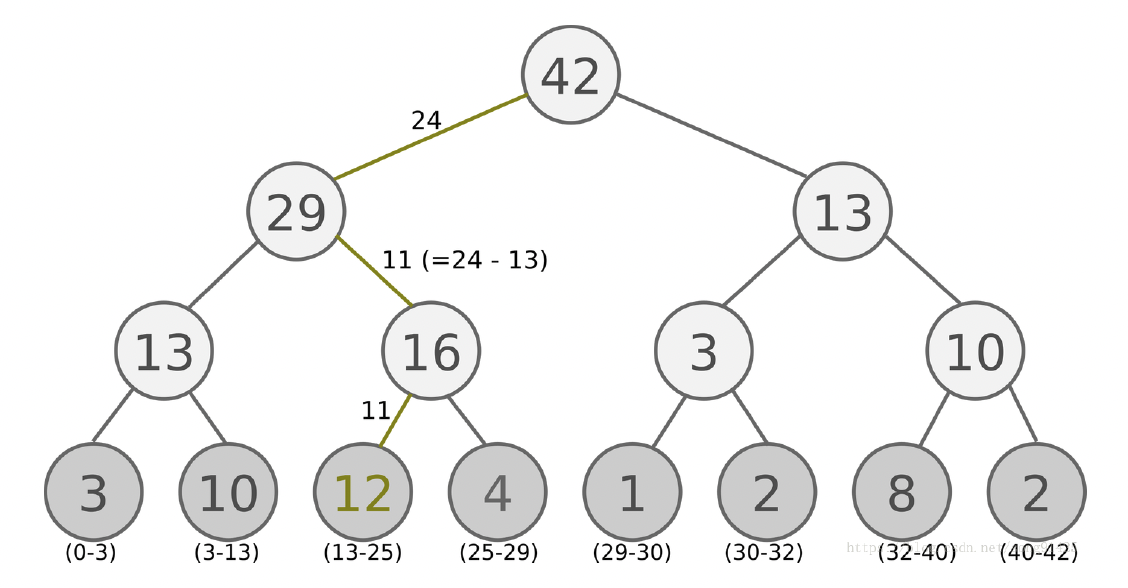
Dueling DQN
将 $q(s,a)$ 拆分成两个部分:与行动独立的值函数 $v(s)$ 和行动依赖的优势函数 $A(s,a)$,即
不过这里存在不可识别的问题,因此考虑
详细内容可参考 Wang 等人(2016)。
Rainbow
Hessel 等人(2017)研究了DQN算法的六个扩展(包括DDQN、Prioritized DDQN、Dueling DDQN等),并对其组合进行了实证研究。实验表明,从数据效率和最终性能方面来说,Rainbow这个组合能够在Atari 2600基准上提供最为先进的性能。
连续行动的Q-Learning
在连续行动下,要采取最优行动计算行动值函数的最大值并不是那么容易,如果在内部循环嵌套一个子随机梯度下降算法会导致算法效率较低。有以下几种可能的选择。
Stochastic Optimization
一个最简单的做法就是从行动分布中采样一组 $(a_1,\dots,a_N)$,然后再选择具有最大 $q$ 值的行动,即
这种方法显然不是很精确,但是非常快,而且可以并行计算。要得到更精确的解可以考虑:
- Cross Entropy Methods:采样 $N$ 个行动后最小化分布之间的交叉熵;
- CMA-ES:基于进化策略算法,能够进行自我调整。
Easily Maximizable Q Functions
在NAF(Normalized Advantage Functions)框架下,我们假定
于是 $\underset{a\in\cal A}{\arg\max}~q(s,a,\pmb w)=\mu(s,\pmb w)$,$\max\limits_{a\in\cal A} q(s,a,\pmb w)=v(s,\pmb w)$。

DDPG(Deep Deterministic Policy Gradient)
DDPG的想法是训练另一网络来近似 $\mu(s,\pmb\theta)\approx\underset{a\in\cal A}{\arg\max}~q(s,a,\pmb w)$,因此只需要找到 $\pmb\theta$ 满足
而这由链式法则 $\dfrac{\text{d}q(s,\mu(s,\pmb\theta),\pmb w)}{\text{d}\pmb\theta}=\dfrac{\text{d}q(s,a,\pmb w)}{\text{d}a}\cdot\dfrac{\text{d}\mu(s,\pmb\theta)}{\text{d}\pmb\theta}$ 立得。
所以DDPG算法如下:
- 采取行动 $a_t$,得到 $(s_t,a_t,s_{t+1},r_{t+1})$,并将其加入 $\cal B$ 中;
- 从 $\cal B$ 中均匀地采样一批 $(s_t,a_t,s_{t+1},r_{t+1})$;
- 计算目标 $\text{target}(s_t)=r_{t+1}+\gamma\max\limits_{a’\in\cal A}q(s_{t+1},\mu(s_{t+1},\pmb\theta’),\pmb w’)$;
- 更新参数 $\displaystyle\pmb w\leftarrow\pmb w+\alpha\sum\limits_t\big(\text{target}(s_t)-q(s_t,a_t,\pmb w)\big)\dfrac{\text{d}q(s_t,a_t,\pmb w)}{\text{d}\pmb w}$;
- 更新参数 $\displaystyle\pmb\theta\leftarrow\pmb\theta+\beta\sum\limits_t\dfrac{\text{d}q(s,a,\pmb w)}{\text{d}a}\cdot\dfrac{\text{d}\mu(s,\pmb\theta)}{\pmb\theta}$;
- 更新 $\pmb w’$ 和 $\pmb\theta’$(例如:Polyak平均);
- 回到第一步。

后记
本文内容来自中国科学技术大学《强化学习》(2022Fall)课件。
如对本文内容有任何疑问,请联系 watthu@mail.ustc.edu.cn。