策略梯度算法与Actor-Critic算法
回顾策略梯度方法是直接对策略 $\pi_\theta$ 进行建模与优化。
定理(策略梯度定理) 对于任何可微策略 $\pi_\theta(a\mid s)$,对于任何目标策略函数 $J=J_1$,$J_{\text{avR}}$ 或 $\dfrac{1}{1-\gamma}J_{\text{avV}}$,策略梯度为
$\displaystyle\nabla_\theta J(\theta)=\mathbb E_{\pi_\theta}\left[q^{\pi_\theta}(s,a)\nabla_\theta\log\pi_\theta(a\mid s)\right].$
证明: 定义目标策略函数
$\displaystyle J(\theta)=\sum_{s\in\mathcal S}d^{\pi_\theta}(s)v^{\pi_\theta}(s)=\sum_{s\in\mathcal S}d^{\pi_\theta}(s)\sum_{a\in\mathcal A}\pi_\theta(a\mid s)q^{\pi_\theta}(s,a).$
考虑
$\begin{array}{rl}
\nabla_\theta v^{\pi_\theta}(s)=&\!\!\!\!\displaystyle\nabla_\theta\left(\sum_{a\in\mathcal A}\pi_\theta(a\mid s)q^{\pi_\theta}(s,a)\right)\\
=&\!\!\!\!\displaystyle\sum_{a\in\mathcal A}\left(\nabla_\theta\pi_\theta(a\mid s)q^{\pi_\theta}(s,a)+\pi_\theta(a\mid s)\nabla_\theta q^{\pi_\theta}(s,a)\right)\\
=&\!\!\!\!\displaystyle\sum_{a\in\mathcal A}\left(\nabla_\theta\pi_\theta(a\mid s)q^{\pi_\theta}(s,a)+\pi_\theta(a\mid s)\nabla_\theta\sum_{s',r}P(s',r\mid s,a)(r+\gamma v^{\pi_\theta}(s'))\right)\\
=&\!\!\!\!\displaystyle\sum_{a\in\mathcal A}\left(\nabla_\theta\pi_\theta(a\mid s)q^{\pi_\theta}(s,a)+\gamma\pi_\theta(a\mid s)\sum_{s'\in\mathcal S}P(s'\mid s,a)\nabla_\theta v^{\pi_\theta}(s')\right),
\end{array}$
令 $\phi(s)=\displaystyle\sum_{a\in\mathcal A}\nabla_\theta\pi_\theta(a\mid s)q^{\pi_\theta}(s,a)$,$d^{\pi_\theta}(s\rightarrow x,k)$ 为策略 $\pi_\theta$ 从状态 $s$ 出发 $k$ 步后到达状态 $x$ 的概率,于是
$\begin{array}{rl}
\nabla_\theta v^{\pi_\theta}(s)=&\!\!\!\!\displaystyle\phi(s)+\gamma\sum_{a\in\mathcal A}\sum_{s'\in\mathcal S}\pi_\theta(a\mid s)P(s'\mid s,a)\nabla_\theta v^{\pi_\theta}(s')\\
=&\!\!\!\!\displaystyle\phi(s)+\gamma\sum_{s'\in\mathcal S}d^{\pi_\theta}(s\rightarrow s',1)\nabla_\theta v^{\pi_\theta}(s')\\
=&\!\!\!\!\displaystyle\phi(s)+\gamma\sum_{s'\in\mathcal S}d^{\pi_\theta}(s\rightarrow s',1)\left[\phi(s')+\gamma\sum_{s''\in\mathcal S}d^{\pi_\theta}(s'\rightarrow s'',2)\nabla_\theta v^{\pi_\theta}(s'')\right]\\
=&\!\!\!\!\cdots\\
=&\!\!\!\!\displaystyle\sum_{x\in\mathcal S}\sum_{k=0}^{+\infty}\gamma^kd^{\pi_\theta}(s\rightarrow x,k)\phi(x).
\end{array}$
令 $\displaystyle\eta(s)=\mathbb E_{s_0}\left[\sum_{k=0}^{+\infty}\gamma^kd^{\pi_\theta}(s\rightarrow x,k)\right]$,回到目标函数,即有
$\begin{array}{rl}
\nabla_\theta J(\theta)=&\!\!\!\!\displaystyle\nabla_\theta\mathbb E_{s_0}[v^{\pi_\theta}(s_0)]=\sum_{s\in\mathcal S}\eta(s)\phi(s)\propto\sum_{s\in\mathcal S}d^{\pi_\theta}(s)\sum_{a\in\mathcal A}\nabla_\theta\pi_\theta(a\mid s)q^{\pi_\theta}(s,a).
\end{array}$
这就证明了策略梯度定理。
利用策略梯度定理,我们就有REINFORCE算法,其中 $q^{\pi_\theta}(s,a)$ 采用蒙特卡洛方法进行估计。
具体来说,考虑一个轨迹 $S_0,A_0,R_1,S_1,A_1,R_2,\dots$,所以
$\displaystyle\nabla_\theta J(\theta)=\mathbb E\left[\sum_{t=0}^T\gamma^tR_{t+1}\sum_{t=0}^T\nabla_\theta\log\pi(A_t\mid S_t)\right].$
由因果性,进一步可以改写为
$\displaystyle\nabla_\theta J(\theta)=\mathbb E\left[\sum_{t=0}^T\left(\sum_{t'=t}^T\gamma^{t'-t}R_{t'+1}\right)\nabla_\theta\log\pi(A_t\mid S_t)\right].$
这就是REINFORCE算法的基本原理。事实上,我们可以考虑更加一般的形式:
$\displaystyle\nabla_\theta J(\theta)=\mathbb E\left[\sum_{t=0}^T\Psi_t\nabla_\theta\log\pi(A_t\mid S_t)\right].$
这里的 $\Psi_t$ 可以有很多种形式:
(1)轨迹的总回报 $\displaystyle\sum_{t'=0}^T\gamma^{t'}R_{t'+1}$;(2)动作 $A_t$ 之后的总回报 $\displaystyle\sum_{t'=t}^T\gamma^{t'-t}R_{t'+1}$;
(3)基准线版本的改进 $\displaystyle\sum_{t'=t}^T\gamma^{t'-t}R_{t'+1}-b(S_t)$;(4)行动值函数 $q^{\pi_\theta}(S_t,A_t)$;
(5)优势函数 $A^{\pi_\theta}(S_t,A_t)$;(6)时序差分残差 $R_{t+1}+\gamma v^{\pi_\theta}(S_{t+1})-v^{\pi_\theta}(S_t)$。
这实际上就是Actor-Critic算法。
深度强化学习中的策略梯度算法
如果将策略梯度视作分类问题,创建虚拟标签
$\pi^\star(a\mid s_t)=\left\{\begin{array}{ll}
1, & a=a_t,\\
0, & \text{otherwise},
\end{array}\right.$
其中 $a_t$ 是在回合 $\tau$ 中状态 $s_t$ 下采取的行动。于是可以采用交叉熵损失
$\displaystyle\text{CE-Loss}=-\sum_{s,a}\pi^\star(a\mid s)\log\pi_\theta(a\mid s)$
作为损失函数来进行神经网络的训练,从而得到最优参数 $\theta$。因此,对极大似然估计方法,梯度为
$\displaystyle\nabla_\theta J_{\text{ML}}(\theta)=\mathbb E\left[\sum_{t=0}^T\nabla_\theta\log\pi_\theta(A_t\mid S_t)\right].$
On-policy
策略梯度算法是on-policy的算法,事实上,
$\displaystyle\nabla_\theta J(\theta)=\mathbb E_{\tau\sim\pi_\theta(\tau)}\left[r(\tau)\nabla_\theta\log\pi_\theta(\tau)\right]\approx\dfrac{1}{N}\sum_{i=1}^N\sum_{t=0}^Tq^{\pi_\theta}(s_{i,t},a_{i,t})\nabla_\theta\log\pi_\theta(a_{i,t}\mid s_{i,t}).$
这里的采样 $\tau\sim\pi_\theta(\tau)$ 在深度强化学习中应用会出问题,效率十分低。
Off-policy
之所以要引入off-policy的策略梯度方法,是因为
- Off-policy策略梯度方法不需要完整的轨迹,它可以利用过去的回合得到高效的算法;
- Off-policy策略梯度方法从行为策略中进行采样,而不是从目标策略中采样,具有一定的探索能力。
具体来说,行为策略是一个确定性策略 $\beta(a\mid s)$,于是目标策略函数就定义为
$\displaystyle J(\theta)=\sum_{s\in\mathcal S}d^\beta(s)\sum_{a\in\mathcal A}q^{\pi_\theta}(s,a)\pi_\theta(a\mid s)=\mathbb E_{s\sim d^\beta}\left[\sum_{a\in\mathcal A}q^{\pi_\theta}(s,a)\pi_\theta(a\mid s)\right],$
其中 $d^\beta(s)=\lim\limits_{t\rightarrow\infty}\mathbb P(S_t=s\mid S_0=s_0,\beta)$ 是 $\beta$ 的平稳分布。此时,策略梯度
$\begin{array}{rl}
\nabla_\theta J(\theta)=&\!\!\!\!\displaystyle\mathbb E_{s\sim d^\beta}\left[\sum_{a\in\mathcal A}\big(q^{\pi_\theta}(s,a)\nabla_\theta\pi_\theta(a\mid s)+\pi_\theta(a\mid s)\nabla_\theta q^{\pi_\theta}(s,a)\big)\right]\\
\approx&\!\!\!\!\displaystyle\mathbb E_{s\sim d^\beta}\left[\sum_{a\in\mathcal A}q^{\pi_\theta}(s,a)\nabla_\theta\pi_\theta(a\mid s)\right]\\
=&\!\!\!\!\displaystyle\mathbb E_\beta\left[\dfrac{\pi_\theta(a\mid s)}{\beta(a\mid s)}q^{\pi_\theta}(s,a)\nabla_\theta\log\pi_\theta(a\mid s)\right],
\end{array}$
其中 $\dfrac{\pi_\theta(a\mid s)}{\beta(a\mid s)}$ 就是重要性采样的权重。注意到中间有一步近似,但这一步并不影响我们收敛到全局最优值。
有了这一结果,我们就可以从 $\beta$ 策略中生成数据,然后利用这些数据来训练 $\theta$,实现了深度学习要求的大量数据的要求,梯度为
$\begin{array}{rl}
\nabla_\theta J(\theta)=&\!\!\!\!\mathbb E_{\beta}\left[\dfrac{\pi_\theta(a\mid s)}{\beta(a\mid s)}q^{\pi_\theta}(s,a)\nabla_\theta\log\pi_\theta(a\mid s)\right]\\
\approx&\!\!\!\!\displaystyle\dfrac{1}{N}\sum_{i=1}^N\sum_{t=0}^T\dfrac{\pi_\theta(a_{i,t}\mid s_{i,t})}{\beta(a_{i,t}\mid s_{i,t})}q^{\pi_\theta}(s_{i,t},a_{i,t})\nabla_\theta\log\pi_\theta(a_{i,t}\mid s_{i,t}).
\end{array}$
深度强化学习中的Actor-Critic算法
A2C
Advantage Actor-Critic(A2C)由策略网络 $\pi_\theta(a\mid s)$ 和价值网络 $v_{\pmb w}(s)$ 构成。具体来说:
- 采取行动 $a_t\sim\pi_\theta(a\mid s)$,得到转移 $(s_t,a_t,s_{t+1},r_{t+1})$;
- 计算TD目标 $y_t=r_{t+1}+\gamma v_{\pmb w}(s_{t+1})$ 和TD误差 $\delta_t=v_{\pmb w}(s_t)-y_t$;
- 更新策略网络参数 $\Delta\theta=\alpha\delta_t\nabla_\theta\log\pi_\theta(a_t\mid s_t)$;
- 更新价值网络参数 $\Delta\pmb w=\alpha\delta_t\nabla_{\pmb w}v_{\pmb w}(s_t)$(这实际上是TD误差关于参数的梯度)。
这里第一步仅仅是用了一步,可以推广到多步,即TD目标改写为
$\displaystyle y_t=\sum_{i=0}^{m-1}\gamma^{i}r_{t+i+1}+\gamma^mv_{\pmb w}(s_{t+m}).$
可以看到REINFORCE算法实际上是A2C算法的一种特例。
A3C
Asynchronous Advantage Actor-Critic(A3C)是A2C的并行版本。在A3C算法中,critic学习价值网络,同时多个actor并行训练策略网络,与环境进行交互,周期性地独立更新全局参数。
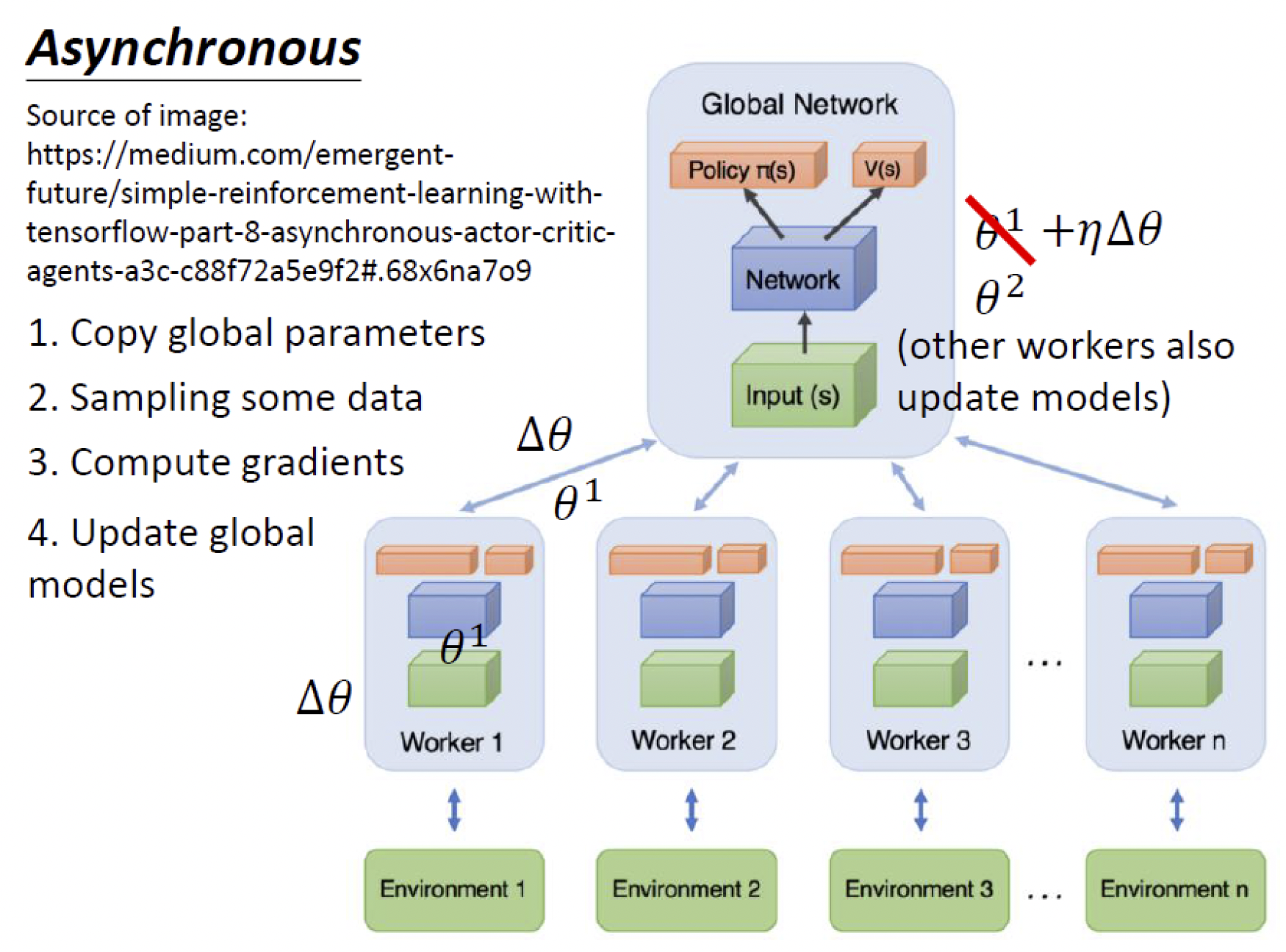
其算法如下图所示。

DPG
Deterministic Policy Gradient(DPG)算法将策略视为确定性策略 $a=\mu_\theta(s)$,而不是在行动空间 $\mathcal A$ 上的一个概率分布,此时策略梯度为
$\begin{array}{rl}
\nabla_\theta J(\theta)=&\!\!\!\!\displaystyle\sum_{s\in\mathcal S}\rho^\mu(s)\nabla_aq^\mu(s,a)\nabla_\theta\mu_\theta(s)\mid_{a=\mu_\theta(s)}\\
=&\!\!\!\!\displaystyle\mathbb E_{s\sim\rho^\mu}\left[\nabla_aq^\mu(s,a)\nabla_\theta\mu_\theta(s)\mid_{a=\mu_\theta(s)}\right],
\end{array}$
其中 $\rho^\mu$ 是 $\mu$ 的状态分布。
将确定性算法与SARSA参数更新融合,可以得到
$\begin{array}{rl}
\delta_t=&\!\!\!\!r_t+\gamma q_w(s_{t+1},a_{t+1})-q_w(s_t,a_t),\\
w_{t+1}=&\!\!\!\!w_t+\alpha\delta_t\nabla_wq_w(s_t,a_t),\\
\theta_{t+1}=&\!\!\!\!\theta_t+\alpha\nabla_aq_w(s_t,a_t)\nabla_\theta\mu_\theta(s)\mid_{a=\mu_\theta(s)}.
\end{array}$
训练轨迹通过随机策略 $\beta(a\mid s)$ 生成,因此状态分布对应于 $\rho^\beta$,从而
$\nabla_\theta J(\theta)=\mathbb E_{s\sim\rho^\beta}\left[\nabla_aq^\mu(s,a)\nabla_\theta\mu_\theta(s)\mid_{a=\mu_\theta(s)}\right].$
注意到这里确定性策略导致对行动的积分项可以略去,所以不需要采用重要性采样。
DDPG
这里从另一个视角看Lec11已经介绍过的DDPG,它实际上是DPG与DQN的结合。
由于我们关心的行动空间此时是连续的,所以无法遍历所有行动来得到 $q$ 值最大的行动,所以想用策略 $\mu(s)=\underset{a\in\mathcal A}{\arg\max}~q(s,a)$ 实现这一效果。 而在实际应用中,则是在 $\mu_\theta$ 的基础上考虑一定的探索:
$\mu'(s)=\mu_\theta(s)+\mathcal N,$
这里的 $\mathcal N$ 是一定的噪音。

TRPO
当策略网络是深度模型时,沿着策略梯度更新参数,很有可能由于步长太大导致策略突然变差,从而影响训练效果。Trust Region Policy Optimization(TRPO)考虑在更新时找到一块信任区域,在这个区域更新策略能够得到安全性保证。
具体来说,首先将目标函数改写为
$J(\theta)=\mathbb E_{s\sim\rho^{\pi_{\theta_\text{old}}},a\sim\pi_{\theta_\text{old}}}\left[\dfrac{\pi_\theta(a\mid s)}{\pi_{\theta_\text{old}}(a\mid s)}\hat{A}_{\theta_\text{old}}(s,a)\right],$
TRPO要求我们最大化这一目标函数,但要满足距离条件:
$\mathbb E_{s\sim\rho^{\pi_{\theta_\text{old}}}}\left[D_{\text{KL}}(\pi_{\theta_\text{old}}(\cdot\mid s)\|\pi_\theta(\cdot\mid s))\right]\leq\delta.$
这样就保证了每次更新目标函数的上升。
PPO
TRPO在求解上比较困难,Proximal Policy Optimization(PPO)算法对其进行了改进,认为 $r(\theta)=\dfrac{\pi_\theta(a\mid s)}{\pi_{\theta_\text{old}}(a\mid s)}$ 应当在1附近的小范围(即 $[1-\varepsilon,1+\varepsilon]$)内,因此PPO的目标函数为
$J(\theta)=\mathbb E\left[\min(r(\theta)\hat{A}_{\theta_\text{old}}(s,a),\text{clip}(r(\theta),1-\varepsilon,1+\varepsilon)\hat{A}_{\theta_\text{old}}(s,a))\right],$
其中 $\text{clip}(x,l,r)=\max(\min(x,r),l)$,即将 $x$ 限制在 $[l,r]$ 区间内。
- 在连续行动空间上,当奖励在有界支撑上衰减时,标准PPO算法不太稳定。
- 在离散行动空间但有稀疏高奖励时,标准PPO算法经常陷入局部最优行动。
- 如果有许多局部最优行动时,PPO得到的策略对初值十分敏感。
解决上述问题也可以类似于TRPO引入KL正则化如下:
$\begin{array}{rl}
J_\text{forward}(\theta)=\mathbb E\left[\dfrac{\pi_\theta(a\mid s)}{\pi_{\theta_\text{old}}(a\mid s)}\hat{A}_{\theta_\text{old}}(s,a)\right]-\beta D_{\text{KL}}(\pi_{\theta_\text{old}}(\cdot\mid s)\|\pi_\theta(\cdot\mid s)),\\
J_\text{reverse}(\theta)=\mathbb E\left[\dfrac{\pi_\theta(a\mid s)}{\pi_{\theta_\text{old}}(a\mid s)}\hat{A}_{\theta_\text{old}}(s,a)\right]-\beta D_{\text{KL}}(\pi_\theta(\cdot\mid s)\|\pi_{\theta_\text{old}}(\cdot\mid s)).
\end{array}$
后记
本文内容来自中国科学技术大学《强化学习》(2022Fall)课件。
如对本文内容有任何疑问,请联系 watthu@mail.ustc.edu.cn。


